Read...

The spatial scales of weather systems run the gamut from planetary scale to microscale. Before we get into defining each specific scale, I should point out that none of them have universally accepted definitions. That's right, the "boundaries" of each size scale can be somewhat murky. Therefore, think of the size scales more as a continuum, instead of having hard, fixed boundaries. In any event, I still want to give you some general guidelines, and in this course, we'll base our definitions on some of the more commonly used criteria. Just keep in mind that the exact boundaries are somewhat artificial.

The planetary scale typically includes long waves, which have wavelengths exceeding 5000 kilometers (about 3000 miles). For example, the analysis of the daily average 500-mb heights on May 10, 2010 (see below), reveals several long waves encircling the Northern Hemisphere. Note the long-wave trough over eastern North America and the long-wave ridge farther downstream over the Atlantic Ocean. Technically speaking, the wavelength of this trough-ridge couplet is the distance between the trough axis over eastern North America and the trough axis off the west coast of Europe (marked by the dashed white lines). This distance is right around 5000 kilometers, so it falls into the planetary scale.

The average daily 500-mb heights on May 10, 2010. Note the long-wave trough and ridge over eastern North America and the North-central Atlantic Ocean, respectively. This long wave qualifies as a feature on the planetary scale.

Credit: Earth System Research Laboratory

Next in our spectrum of spatial scales is the synoptic scale, which refers to features ranging from about 1000 kilometers (about 600 miles) to 5000 kilometers. However, I want to again emphasize some murkiness here. Many meteorologists take the smaller end of the synoptic-scale to be 2000 kilometers (about 1200 miles), so just realize that when you encounter features between 1000 kilometers and 2000 kilometers, you may find some disagreement about their classifications. Regardless of that murkiness, you should already be familiar with many synoptic-scale features. The mid-latitude high- and low-pressure systems that you've studied in previous courses, along with warm and cold fronts associated with mid-latitude cyclones are typically considered synoptic scale features, when measured by their lengths.

That qualifier I added at the end, "when measured by their lengths" is very important because whenever you're attempting to categorize the scale of weather systems, always keep in mind that your classification depends on the axis along which you're measuring. For example, if we look at the surface analysis from 03Z on August 23, 2015, the length cold front that snakes from the Upper Midwest back through the Rockies qualifies as synoptic scale (and that's typical of most cold fronts). However, cross-sectional views of fronts associated with mid-latitude cyclones reveal that the air motions along (and near) the front are much smaller, and are typically less than 1000 kilometers, so they're smaller than synoptic scale.

The bottom line is that that any classification of the spatial scale of weather systems often depends on the horizontal axis along which you focus your analysis. You may find that along its major (longer) axis, a feature fits into one size scale, but along its minor (shorter) axis, a feature fits into another size scale. It's fairly common for surface fronts to be synoptic-scale in terms of their lengths (major axis), but have vertical motions that occur across the front (minor axis) which qualify as mesoscale.

Speaking of the mesoscale, it's time to finally complete our definition. Mesoscale weather features are between roughly 2 kilometers (1.2 miles) and 1000 kilometers. Many various mesoscale weather features exist, and we'll study a lot of them in this course. For now, however, we'll use a thunderstorm as a common example of a mesoscale weather feature. As you'll soon see, meteorologists actually subdivide the mesoscale even further, and we'll get into more details on that in the next section.

Finally, microscale weather features are those that span less than two kilometers. Even though we'll study tornadoes in depth in this course, technically, most of them are microscale features. Very few tornadoes exceed the two kilometers in width needed to qualify them as mesoscale features.

That's a quick run down on spatial scales from planetary scale to microscale. Up next, we'll take a closer look at how meteorologists subdivide the mesoscale. Before you move on, however, an important skill that you need to develop is the ability to identify features on weather maps, and classify their size scale properly. Check out the Key Skill section below for some important discussion and tips about properly sizing things up.

Read...

In the previous section, we defined the mesoscale as ranging from 2 kilometers to 1000 kilometers. However, the reality is that weather features toward the small end of that range (nearly microscale) can behave much differently from those near the large end of that range (nearly synoptic scale). Therefore, meteorologists break the mesoscale down into three subdivisions, as illustrated in the image below:

The three subdivisions of the mesoscale -- the meso-γ (meso-gamma) scale (2 to 20 kilometers), the meso-β (meso-beta) scale (20 to 200 kilometers), and the meso-α (meso-alpha) scale (200 to 1000 kilometers).

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0 

At the large end of the mesoscale, we have the meso-α (meso-alpha) scale (200 to 1000 kilometers), followed by the meso-β (meso-beta) scale (20 to 200 kilometers), and the meso-γ (meso-gamma) scale (2 to 20 kilometers) at the small end of the mesoscale.

A tropical cyclone, which is the generic name for a low-pressure system that forms over tropical seas (it has a distinct low-level cyclonic circulation), is representative of a meso-α (meso-alpha) weather system because its spatial scale usually falls within 1000 kilometers. For example, the satellite-based radar and cloud image below shows the structure and spatial scale of Hurricane Frances on August 30, 2004. Given the distance scale along the bottom of the image, you can see that Frances easily qualified as a meso-α feature (it spanned about 400 kilometers).

A satellite-based radar and cloud image of Hurricane Frances at 10:21Z on August 30, 2004 (to the north of the Leeward Islands). Tropical storms and hurricanes typically qualify as meso-α features.

Credit: NASA-TRMM

Of course, tropical cyclones vary markedly in size, and indeed, not all tropical cyclones are meso-α features. Certainly, most are meso-α features, but we can't make sweeping generalizations to say that they all are, and that's the case with many atmospheric phenomena. On the one hand, the very largest hurricanes can cross the threshold into the synoptic scale. Hurricane Sandy (2012), for example, was one such storm that spilled over into the synoptic scale since its circulation exceeded 1000 kilometers. Meanwhile, the smallest hurricanes are small enough to be considered meso-β. Hurricane Danny (2015), for example, was a pipsqueak by hurricane standards (it was one of the smallest Atlantic hurricanes on record). Danny's area of winds greater than 34 knots (tropical-storm force) had a diameter less than 100 miles (160 kilometers), classifying the storm as meso-β.

Speaking of the meso-β subdivision, I offer a single band of lake-effect snow that formed over Lake Michigan on February 20, 2008 (check out the 1553Z image of radar reflectivity from Grand Rapids, Michigan, below). Obviously, I'm referring to the length of the band of snow when I classify the band as a meso-β feature.

The 1553Z radar reflectivity from Grand Rapids, Michigan, on February 20, 2008, shows a single band of lake-effect snow over Lake Michigan. Lake-effect bands typically qualify as meso-β features.

Credit: Used by permission, Gibson Ridge Software / National Weather Service

Other examples of typical meso-β features are sea and lake-breeze circulations, which we'll study later in the course. An interesting feature associated with this lake-effect band was the swirl toward its southern edge. Appropriately, that signature was from an aptly named, "mesovortex" that formed over the southern bowl of Lake Michigan (you can think of a mesovortex as a meso-γ low-pressure system). You'll encounter mesovortices again later in the course, as well.

Taking another step down to the meso-γ scale, we finally get to the typical scale of individual thunderstorm cells. For example, this supercell thunderstorm (a supercell is just a thunderstorm with a persistent, rotating updraft) over Southern Maryland on April 28, 2002 qualifies as a meso-γ feature. The photograph was taken on a commercial flight by a former Penn State meteorology student! Along its destructive path, this storm spawned large hail and an F4 tornado on the Fujita Tornado Damage Scale. The tornado reached F4 intensity over La Plata, Maryland, where it killed three people and injured 100. The La Plata twister was the strongest ever to hit Maryland since weather records began. For more on the Fujita Tornado Damage Scale, check out the Explore Further section below, if you're interested.

(Left) The La Plata tornado over Chesapeake Bay after it rampaged through La Plata. At this point, the tornado was an F2 (based on damage assessments at nearby shore communities). (Right) In the aftermath of the F4 twister that struck La Plata, Maryland, on April 28, 2002, NASA's EO-1 satellite captured the swath of destruction through the town.

Credit: National Weather Service / NASA

I should point out that the thunderstorm that spawned the tornado is the mesoscale feature, not the tornado. This tornado (and the vast majority of tornadoes) are actually microscale features. To give you a better sense of the scale of this tornado, focus your attention on the satellite image on the right above. Clearly, the width of the twister's damage swath was confined to several rows of houses, indicating that the tornado was only a few hundreds of meters across. Although this course is about mesoscale forecasting, we will, of course, study microscale features as they relate to the parent mesoscale weather systems.

Before we move on, I want to point out that you might also occasionally encounter the term "storm scale" around the World Wide Web. Most informal definitions suggest that "storm scale" refers to the "scale of individual thunderstorms" and have equated storm scale with the meso-γ subdivision. Yet, I have also seen "storm scale" linked to the meso-β subdivision. The bottom line is that no official guidelines regarding the use of "storm scale" exist, so I won't use the term in this course, and will stick with the three subdivisions shown above.

Up next, we'll shift from talking about spatial scales to talking about time-scale issues involving mesoscale systems. But, before we move on, check out the Key Skill box below, which will give you some exposure to reference measurements and the mesoscale subdivisions.

Read...

Now that you have a good handle on where the mesoscale fits into the range of spatial scales, it's time to shift gears and talk about time scales. To launch our discussion, let's cover a couple of definitions:

• The Lagrangian time scale (or "time scale" for short) of a weather system, is the amount of time it takes for an air parcel to move through the entire system. The word, "Lagrangian," means that we follow an air parcel on its trek through the weather system.
• The duration of a weather system refers to its lifetime -- how long the feature itself lasts.

To understand the difference between the time scale of a weather system and its duration, I'll use a supercell thunderstorm as an example. Recall that supercell thunderstorms possess a persistent, rotating updraft that sometimes (although not always) produces a tornado. The duration of most supercells is, as a general rule, between one and four hours, which means that most supercells "live" for one to four hours, before they dissipate. I should note, however, that long-lived supercells can last as long as eight hours.

Now, what about the time scale of a typical supercell? For starters, check out this nifty computer simulation of a tornadic supercell showing the motions of various streams of air that flow through the storm. It's clear from the animation that individual air parcels flow all the way through a supercell during its lifetime. The peach-colored ribbons indicate the paths that air parcels took through the updraft of an idealized supercell.  Relative to the moving storm, air parcels enter the storm near the ground, rise, and then get whisked downstream by westerly winds near the top of the storm. The trip through the updraft usually lasts about 20 minutes, which serves as a fairly good approximation for the Lagrangian time scale of a supercell. In case you're wondering, the blue ribbons follow the paths of air parcels entering the rear of the storm and ultimately sinking toward the ground.

A single frame from a computer simulation of a supercell thunderstorm. The peach-colored ribbons indicate the paths that air parcels took through the storm's updraft (relative to the moving storm).

Credit: University of Illinois

The bottom line here is that the time scale of a weather feature might be a lot different from its duration. Think back to some mid-latitude weather features that you studied previously.  A jet streak, for example, moves along in the flow at 300 mb at 30 to 50 knots, on average, during the winter. But, individual air parcels are moving much faster, and they accelerate right through the jet streak. In other words, a jet streak's duration is much longer than its Lagrangian time scale.

We can apply similar thoughts to shortwave troughs. The troughs themselves move along in the synoptic-scale flow, but individual air parcels move right through the shortwave (causing divergence downstream, if you recall). So, because the shortwave lasts much longer than the amount of time it takes for a parcel to travel through it, the duration of a shortwave trough is longer than its Lagrangian time scale.

Most of the references that you'll run across will typically categorize weather systems by their spatial scales and their duration (not their Lagrangian time scales). But, I like to make a clear distinction here because we'll talk a lot this semester about how air parcels move relative to the parent weather systems.

Still, there's a general relationship between the size scale of a weather feature and its duration. The duration of a dust devil (photograph courtesy of David DiBiase), a microscale rapidly rotating wind that is made visible by the dust, dirt or debris it picks up, is typically on the order of a few minutes or shorter. Under optimum conditions, dust devils can last as long as a few tens of minutes, but such "long-lived" dust devils are rare. On the other hand, keeping in mind that the duration of a supercell thunderstorm (a meso-γ or meso-β feature) is typically one to four hours, you should now get the impression that, as the spatial scales of weather features decrease, so do their duration.

To confirm your impression, check out the schematic below; it displays the spatial scales (horizontal axis) and duration (vertical axis) of selected weather features. Pay close attention to relationship between spatial scale and duration. As a general rule (with a few exceptions), the smaller the spatial scale, the shorter the duration.

A schematic showing the typical spatial scale and duration of selected weather features. In the case of synoptic-scale fronts, the indicated spatial scale corresponds to a representative length (not a width). Similarly, the indicated spatial scale of dry lines also corresponds to a representative length. Full-sized image.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0 

Given the relatively short duration and small spatial scale of mesoscale phenomena, forecasters require computer models that are higher resolution and incorporate hourly observations so as to more accurately model rapidly evolving weather patterns. We'll investigate in the next section.

Read...

On February 10, 2009, supercells erupted over parts of the Southeast States. The 2238Z radar reflectivity (below) from Maxwell Air Force Base (KMXX) indicates the rather small coverage of the severe thunderstorms over eastern Alabama and western Georgia. Only the most favorable local environments supported deep, moist convection at this time. Of course, there was no way to predict exactly where these supercells would have developed, but accurately identifying the general area (Alabama, Georgia and parts of the surrounding states) where storms were likely to "initiate" on this day would have been a pretty good forecast. It turns out that these storms spawned several reports of tornadoes and numerous reports of large hail across the region.

The 2238Z radar reflectivity from Maxwell Air Force Base (KMXX) in south-central Alabama on February 10, 2009. By this time, discrete supercells had erupted over parts of eastern Alabama and western Georgia, producing severe weather.

Credit: Used with permission, Gibson Ridge Software / National Weather Service

To successfully identify regions at risk for severe thunderstorms, forecasters first assess the background synoptic-scale pattern by looking at progs from models like the ones you learned about in your previous studies (the GFS, NAM, or others). Assessing the "big picture" from these models is a crucial step in the forecasting process. But, for outbreaks of thunderstorms like the one shown above, these models have some serious flaws. One is that important convective processes are occurring on spatial scales that are smaller than the model's grid-point scheme. The end result is that convection in these models is greatly oversimplified (formally, "parameterized"), which leads to struggles with forecasts for convective precipitation.

Another major problem stems from the fact that, as you just learned, many mesoscale weather features have a relatively short duration. Supercell thunderstorms typically last one to four hours before dissipating (some other types of thunderstorms last less than one hour). But, models like the NAM and GFS are only initialized every six hours (00Z, 06Z, 12Z, and 18Z).

In terms of mesoscale weather, a lot can change in six hours! This relatively long time lag between successive runs, in addition to the inability to infuse hourly observations into the operational GFS and NAM, make these two models less viable for predicting the changing, smaller-scale environments that might favor the initiation of  thunderstorms in the next hour (or even a couple of hours).

Forecasters require "mesoscale" models, with a fine spatial resolution, that are continually updated with timely weather observations so that they can more reliably refine and update their forecasts as weather conditions change in time. Do such models exist? Indeed they do. In 2012, NCEP implemented the Rapid Refresh Model (RR), a short-range model that incorporates GFS forecast data and an analysis / assimilation system to update the model with hourly observations. The Rapid Refresh Model runs every hour, providing crucial short-range forecasts. Forecasters at the Storm Prediction Center, as well as forecasters in the aviation community, frequently incorporate RR analyses (0-hour forecasts) and predictions into their forecasting routines.

The RR model provides data that have a relatively high resolution in space and time (forecasts are available at one-hour intervals). There's also a high-resolution version of the Rapid Refresh that mesoscale forecasters use operationally (the High-Resolution Rapid Refresh or, more simply, the HRRR). For the record, the HRRR model has an even higher spatial resolution, and offers forecasts at 15-minute intervals (read more about the details of the HRRR, if you're interested).

Models like the RR and HRRR have a couple of key advantages. First, because they're initialized every hour, they're more "in touch" with rapidly changing weather situations than models that are initialized every six hours (like the GFS and NAM). Second, with forecast intervals of an hour or less, the RR and HRRR are able to depict the evolution of mesoscale weather systems with greater detail than models having longer forecast intervals.

Furthermore, convection in the the HRRR is not parameterized. It has a sufficiently high spatial resolution that it can actually simulate real convection. Such models are called "convection allowing" models and need to have a grid spacing no larger than four or five kilometers. Because it doesn't have the great oversimplifications that come with convective parameterizations in coarser models, the HRRR is able to depict much more realistic convective structures. As you can see from the HRRR forecast below, its prediction of radar reflectivity looks pretty realistic, doesn't it?

The six-hour forecast of reflectivity from the 17Z run of the High Resolution Rapid Refresh Model on April 27, 2011 (valid at 23Z), accurately predicted the timing, location, and structure of a squall line moving eastward across northern Pennsylvania and western New York.

Credit: NCEP

In the six-hour forecast of radar reflectivity from the 17Z run of the HRRR on April 27, 2011, valid at 23Z (shown above) note the placement and structure of the narrow squall line in western New York and northern Pennsylvania. Now, compare the forecast to the actual 23Z mosaic of composite reflectivity. As you can clearly see, the HRRR had an awesome forecast, capturing the timing and structure of the squall line really well. On the other hand, the HRRR didn't predict the severe storms that formed out ahead of the squall line at all. The HRRR forecast also had problems in Maryland, Ohio and West Virginia, so this forecast was far from perfect.

I hope this example makes it clear that even though such "convection-allowing" models create detailed, realistic-looking convective structures, that does not mean their solutions are always accurate. Indeed, while such models are skillful in predicting the mesoscale details and structure of convection, they do not show consistent skill in predicting the exact timing or location of individual convective cells.

Another problem with "convection-allowing" mesoscale models is that they are prone to huge run-to-run variability (successive solutions may look nothing alike). To combat the large run-to-run variability, forecasters often look for a degree of consistency in three consecutive runs of the HRRR. If the model's solution is similar for three runs in a row, then forecasters have a bit more confidence in the solution. Researchers involved in the Vortex2 project routinely weighed HRRR forecasts to help them formulate plans to intercept storms. If the HRRR was producing consistent solutions for three consecutive runs, chasers would adjust their intercept plans accordingly.

Because these mesoscale models require great computer power to run, they are only run over a short forecast period (a day or less for most runs). Furthermore, their performance is somewhat at the "mercy" of the GFS model's initialization. Remember that the GFS feeds its initial conditions into the Rapid Refresh, so any major errors in the GFS initialization will be transferred into the Rapid Refresh, which can wreak havoc on its forecast accuracy.

Regardless of these limitations, the analyses and forecasts based on the Rapid Refresh Model are still often useful for timely short-range mesoscale prediction. For much of our work in this course, we'll focus on real-time mesoanalyses from the Rapid Refresh model available on SPC's Web site. As outbreaks of severe weather unfold you can rely on these SPC analyses to gain insight about the background synoptic and mesoscale environments.

To give you an example of the types of analyses that are available, check out the SPC mesoanalysis of vertical wind shear between the ground and an altitude of six kilometers over Deep South at 23Z on April 27, 2011. Vertical wind shear refers to a change in wind speed and / or direction with increasing altitude, and it's an important variable in determining the organization and longevity of thunderstorms that develop. On this particular date, very strong vertical shear existed over the Deep South, which played a role in one of the biggest tornado outbreaks in U.S. history that occurred over the region.

The 23Z analysis of vertical wind shear (in knots) between the ground and an altitude of six kilometers over the Deep South on April 27, 2011.

Credit: Storm Prediction Center

Later on, we'll get into the basics on how you can interpret these and other mesoanalysis images, and discuss their connections to the development of deep, moist convection. If you're interested in seeing more about this outbreak, and getting some links where you can access RR and HRRR forecasts, check out the Explore Further section below. Before we end this lesson, however, allow me to introduce the 3-kilometer NAM, which also has some utility for creating short-term mesoscale forecasts. Read on.

Read...

The Rapid Refresh (RR) and High-Resolution Rapid Refresh (HRRR) aren't the only "mesoscale models" available. The National Centers for Environmental Prediction also run high-resolution, convection-allowing versions of models you're already familiar with, which also have use in mesoscale forecasting.

One such model is the NAM. For its high-resolution output, the NAM employs "one-way" smaller nests within the larger outer model domain. Within each nest, the model computes forecasts concurrently with the 12-km NAM parent run. For the record, "one-way nested" means that the inner (nested) model domain receives its lateral boundary conditions from the outer domain, but it does not feed back any information to the outer domain. In other words, the outer domain is not affected by the nest.

The parent 12-kilometer domain of the NAM, along with its three-kilometer nests for CONUS, Alaska, and Hawaii / Puerto Rico, respectively. The smallest rectangles represent very high-resolution nests for predicting fire weather.

Credit: National Centers for Environmental Prediction

The nested domains within the parent NAM have higher resolutions, with three-kilometer nests covering the contiguous U.S., Alaska, Hawaii and Puerto Rico (shown above). The resolution of the internal nests of the NAM is sufficiently high to realistically simulate convection, so while convection is parameterized in runs of the parent 12-km NAM, it's not in the higher-resolution forecast nests. In case you're wondering, the small unlabeled boxes in the image above represent small nests with even higher resolution that are used for predicting fire weather.

The GFS, on the other hand, actually runs on a dynamic model core called the "FV3" ("Finite Volume Cubed Sphere"), which runs on a "flexible" grid. The flexible grid gives modelers options for running higher-resolution versions that can realistically simulate convection over parts of the globe. The model also has the ability to run higher resolution "two-way" nests within its global domain (two-way nests receive their lateral boundary conditions from the outer domain and can feed back some information to the outer domain).

So, are the high-resolution versions of the NAM and FV3 every bit as useful as the HRRR? Not exactly. There's a key difference between the two. While the HRRR is initialized every hour, the high-resolution FV3 and NAM are still only initialized every six hours (06Z, 12Z, 18Z, and 00Z). The high-resolution FV3 and NAM do have forecast intervals of one hour, but they do not get infused with hourly surface observations, which makes them less viable for predicting the small-scale rapidly changing environments that may favor the initiation of thunderstorms.

While the high-resolution FV3 and NAM produce forecasts with realistic-looking convective structures (like in the example below), the same caveats that went along with HRRR forecasts apply. Just because the forecasts look realistic doesn't mean they're accurate, and remember, the fact that the high-resolution FV3 and NAM are only initialized every six hours is a notable drawback. On the flip side, one advantage to these models is that their forecasts go out a few days into the future, which is longer than forecasts from the RR and HRRR. Like with the HRRR, the timing and exact location of individual thunderstorms are often incorrect in high-resolution FV3 and NAM forecasts, but they can still give useful insights into the general coverage and structure of thunderstorms.

The 31-hour forecast of radar reflectivity and MSLP valid at 19Z on May 11, 2023 (from the run initialized at 12Z on May 10) from the high-resolution version of the FV3. Since the high-resolution FV3 does not parameterize convection, its forecasts include realistic-looking convective structures.

Credit: Tropical Tidbits

For comparison with the forecast prog above, the corresponding forecast of radar reflectivity and MSLP from the high-resolution NAM had general similarities to the high-resolution FV3 forecast, but lots of differences in the finer details of convective placement and structure.

Given the differences that regularly occur in high-resolution model output, high-resolution ensemble forecasts can also be of great use, and indeed, NCEP has developed the High-Resolution Ensemble Forecast (HREF) system for mesoscale forecasting. The HREF is comprised of HRRR forecasts, along with high-resolution versions of the NAM, FV3, and other convection-allowing models primarily used by the research community. So, mesoscale forecasters have multiple options for convection-allowing guidance and even a convection-allowing ensemble of models!

If you're interested in accessing forecasts from high-resolution, convection-allowing models, check out the Explore Further section below. Otherwise, we'll wrap up our introduction to mesoscale meteorology with a brief Case Study of a tornado outbreak, which illustrates the connections between spatial scales and the utility of real-time mesoscale model analyses. Read on.

Read...

From a weather forecaster's perspective, predicting thunderstorms and severe weather is always challenging (for a variety of reasons that we'll gradually uncover in this course). Seasoned forecasters develop their own forecasting routines and favorite tools that help to approach the problem in the most consistent way possible. In time, you'll develop your own specific approach and favorite tools for forecasting thunderstorms, but your routine should certainly include:

• getting a firm handle on the big picture (synoptic-scale weather pattern) at the surface and aloft
• getting a sense for overall instability and the potential for strong thunderstorm updrafts
• assessing the magnitude and role of vertical wind shear

While these items are listed as separate bullet points, the reality is that they're all intertwined. Aspects of the big picture impact the potential for strong updrafts as well as the magnitude and role of vertical wind shear, all of which are crucial pieces of any forecast for thunderstorms. In order to see how the big picture impacts the potential for strong updrafts and the magnitude of vertical shear (one of the overarching goals of this lesson), we have to cover a few basics first.

We'll start by covering how forecasters assess the potential for strong updrafts, and doing so requires tackling a few definitions. This discussion requires a good basic knowledge of skew-T diagrams and associated concepts, which you've studied previously. If you're rusty on these topics, I strongly recommend that you spend some time reviewing skew-T basics from Lesson 6 of METEO 101. The basics that you learned previously about how to read information and move parcels on skew-Ts will be absolutely critical in this discussion and our deeper look at skew-Ts later on, so don't skimp on any review time you might need!

With that caveat out of the way, let's start with a few definitions.

The Level of Free Convection

Recall from your previous studies that the lifting condensation level (LCL) is the level where net condensation begins in a lifted parcel. If the parcel continues to rise above the LCL (there's no guarantee it will do so), it now cools at a reduced rate -- the moist adiabatic lapse rate -- marked by the thin blue curve in the image below. If something keeps forcing the parcel to rise (lifting from low-level convergence is one possibility), eventually, the parcel reaches an altitude where its temperature equals the temperature of the environment. Assuming the air parcel rises slightly above this altitude, it becomes positively buoyant, and accelerates upward, setting the stage for deep, moist convection. In light of this convective scenario, meteorologists refer to the altitude where the air parcel first becomes positively buoyant above the LCL as the Level of Free Convection (LFC). In this context, the adjective, "free", means that the positively buoyant parcel will rise freely through a deep layer of the troposphere. No further lifting by an external force is required.

If a parcel is forced to rise moist adiabatically above the LCL, eventually it reaches the LFC, the point above which the parcel becomes positively buoyant and will accelerate upward on its own.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 

You may be asking yourself, "is there always an LFC?" The answer is a resounding, "no." For example, take a look at this sounding from Pittsburgh, Pennsylvania at 12Z on January 6, 2016. A couple of things should jump out at you immediately: First, the lower troposphere is overwhelmingly stable and dry. It was warmer at 700 mb than it was at the surface at this time! Could a parcel lifted from the surface ever become positively buoyant (warmer than its environment) through a deep layer? Absolutely not! Check out this annotated sounding showing the path a parcel would take from the surface to its LCL (not far above the surface), and then lifted moist adiabatically. The parcel is always to the left of the temperature sounding, so it's colder. In other words, even with Herculean lifting, a parcel will never become positively buoyant. It has no LFC.

Even though this particular example came from a location in a cold, dry, Arctic air mass in the winter, the environment may not have an LFC at any time of year -- even in summer, when it's warm and humid. The presence of an LFC (or lack thereof) and its altitude depend largely on lapse rates and low-level temperatures and dew points (we'll explore these issues more shortly).

Equilibrium Level and CAPE

Once a parcel becomes positively buoyant above its LFC (assuming an LFC exists and the parcel makes it to that level), where does the positive buoyancy stop? The answer is called the "equilibrium level." Formally, the Equilibrium Level (EL) is the altitude above the Level of Free Convection where the temperature of a positively buoyant parcel again equals the temperature of its environment (the EL often occurs near the tropopause).

With the LFC and EL safely tucked under our learning belts, we're ready to assess the potential for strong updrafts. On skew-Ts (plotted from radiosonde measurements or model forecasts), CAPE, which stands for Convective Available Potential Energy, is simply the area between the temperature sounding and the local moist adiabat that a lifted air parcel follows between the Level of Free Convection (LFC) and the Equilibrium Level (EL). The positive area on the idealized skew-T near the top of this page (shaded in green) represents CAPE. Of course, CAPE is zero whenever there isn't any surface-based LFC (it's way too stable for air parcels lifted from the ground to become positively buoyant).

So, what does CAPE mean in a practical sense? Let's start with the idea of "Potential Energy". Quite simply, the word "Potential" refers to the possibility that air parcels lifted from the surface make it to the LFC. What about "Energy?" If air parcels lifted from the surface are able to reach the LFC, they become positively buoyant and accelerate upward through a relatively deep layer of the troposphere thanks to the temperature difference between a parcel and its surroundings, which paves the way for deep, moist convection. In light of this process, CAPE (positive area on a skew-T) is a proxy for the total possible amount of kinetic energy that an air parcel can gain between the LFC and the equilibrium level because of its positive buoyancy. The parcel's positive buoyancy is determined by the size of the temperature difference between a parcel and its surroundings, which governs the magnitude of the parcel's upward acceleration, a relationship which you can explore in the interactive tool below.

Interpreting and Using CAPE

Whenever you're working with CAPE, you should always be aware of the proper units. For the record, the units of CAPE are Joules (a unit of energy) per kilogram (J/kg). How can we interpret values of CAPE? In general, you should treat values of CAPE between 0 and 1000 Joules per kilogram as small. When you see CAPE values higher than 2500 Joules per kilogram, think large. But, I wouldn't get carried away with small and large values of of CAPE, because severe thunderstorms (and tornadoes) can and do occur with small values of CAPE (only a few hundred Joules per kilogram). On the other hand, sometimes environments with large values of CAPE (well over 2500 Joules per kilogram) fail to yield a single thunderstorm!

You'll often see CAPE described as "an overall measure of instability in the troposphere." But, treating CAPE this way has some problems. When CAPE is really high and thunderstorms fail to materialize (air parcels lifted from the surface never make it to the LFC), equating CAPE with instability is, at the very least, misleading because some parcels were nudged upward and didn't continue rising as they would in an unstable situation (they weren't forced up far enough to reach the LFC). Plus, the general public tends to equate instability with thunderstorms, so it's wise to avoid using instability to describe CAPE. When you see tables describing CAPE values on the Internet, I wouldn't put much stock in them.

So how should you think about CAPE? I like to treat CAPE as a measure of the potential for strong updrafts. If air parcels lifted from the surface reach the LFC in an environment with CAPE (especially moderate to high CAPE), they accelerate upward, acquiring kinetic energy and forming strong updrafts in developing thunderstorms. If air parcels don't make it to the LFC in an environment with high CAPE, there certainly was a potential for strong updrafts, but they never materialized.

The moral of this story is that there just isn't any universal way to interpret values of CAPE. While CAPE helps forecasters assess the potential for strong updrafts, specific values of CAPE do not guarantee that thunderstorm updrafts will actually form, and cannot be connected to specific updraft speeds. For more of a quantitative look at the connection between CAPE and updraft speeds, check out the materials in the Explore Further section below.

Indeed, to interpret CAPE you must take into account climatology, the season, and the prevailing weather pattern. To see what I mean, consider that values of CAPE along the West Coast are, on average, much smaller than average values over the Middle West. Moreover, CAPE is usually smaller, on average, during winter than it is during spring and early summer.

Ultimately, what determines whether or not strong updrafts will actually materialize if CAPE is present? Let me introduce "Convective Inhibition."

Convective Inhibition

Convective Inhibition (CIN) is a proxy for the amount of energy needed to lift a parcel to its LFC. So, if CIN is great, and lift rather weak, thunderstorms probably won't happen because parcels won't make it to the LFC and accelerate upward. On an idealized skew-T (see below), CIN is the area between the temperature sounding and the dry adiabat / moist adiabat followed by a lifted parcel on its way to its LFC. CIN is represented by the negative area (in red).

A sounding showing the spatial relationship between the LFC and negative area. Also known as Convective Inhibition (CIN), this area is directly proportional to the amount of energy required to lift an air parcel to its LFC.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 

In the idealized skew-T above, the temperature inversion near 850 mb, and the stable layer (small lapse rates) just above it are responsible for a large chunk of the CIN (the negative area shaded in red). To give you an idea of how to interpret CIN values, keep in mind that because CIN is a "negative area," its values are negative, and the more negative the number, the greater the CIN. In general, you can rank CIN values between 0 and minus 25 Joules per kilogram as weak inhibition. CIN values between minus 25 and minus 50 Joules per kilogram typically qualify as moderate. When you see CIN values of at least minus 50 Joules per kilogram or more, think large inhibition.

As it turns out, CIN can be reduced. How's that? In short, the synoptic-scale weather pattern helps to prime local environments for deep, moist convection by reducing CIN primarily via the following three processes:

• low-level heating
• low-level moistening
• synoptic-scale lift

We'll be exploring how synoptic-scale lifting can reduce CIN throughout this lesson, but the role of low-level heating and moistening in reducing CIN are fairly intuitive. For starters, check out this interactive tool showing how low-level heating reduces CIN (pink shading indicates CIN). In a nutshell, heating of the ground and the overlying layer of air moves the lower portion of the temperature sounding toward increasing temperatures (to the right). Meanwhile, the lapse rate in the gradually deepening boundary layer trends toward dry adiabatic, reducing CIN. Also note how the LFC lowers and CAPE (positive area) increases with time in response to low-level heating.

How does low-level moistening reduce CIN? This interactive tool illustrates the consequences of low-level moistening for CIN. In essence, moistening moves the lower portion of the dew-point sounding to the right toward higher dew points. Increasing moisture causes the LCL to lower because an increase in moisture means that air parcels need not rise as far to achieve net condensation. Moreover, note that the LFC also lowers and CAPE (positive area) increases. And, of course, the lapse rate in the well-mixed boundary layer remains dry adiabatic.

These first two cases should not surprise you because increasing surface temperature and dew points ultimately translates to an increase in energy that's available for deep, moist convection. But, before we move on, I want to make an important point: If you're thinking that CIN must be zero for thunderstorms to initiate, wipe this notion from your mind. It's incorrect. Some CIN usually exists when thunderstorms erupt (but its magnitude is fairly small). Overcoming existing CIN is a major theme that we'll cover throughout this lesson.

To access real-time model analyses of CAPE and CIN, SPC's Mesoscale Analysis Page provides a great resource. Under the "Thermodynamics" menu, you'll find several "varieties" of CAPE. The most basic form, that we covered on this page, is "Surface-Based" CAPE. We'll cover some of the other types later in the course (and one in the Explore Further section below).

While forecasters use CAPE as a tool to assess the potential for strong updrafts, they look at environmental lapse rates in the lower half of the troposphere to get a more direct sense for the instability that exists. Let's investigate further.

Read...

In the previous section, you learned that CAPE helps forecasters to assess the potential for strong updrafts, but doesn't directly tell us about atmospheric stability. If you want to assess the stability of a specific layer of the atmosphere, the key is lapse rates. Therefore, forecasters use lapse rates in concert with CAPE to assess stability and the potential for strong updrafts.

In your previous studies, you learned that the lapse rate is the change in temperature with altitude in any given layer of air. As a general rule, the greater the decrease in temperature with height, the greater the likelihood for convective overturning and the development of thunderstorm updrafts. So, how do we assess how "large" or "small" environmental lapse rates are in a given situation? Start by keeping in mind some key "benchmark" lapse rates that will help you as you assess the stability of specific atmospheric layers:

• the dry-adiabatic lapse rate: 9.8 degrees Celsius per kilometer (you can use about 10 degrees Celsius per kilometer as a proxy)
• the moist-adiabatic lapse rate: roughly 6 degrees Celsius per kilometer, but recall that this lapse rate is not constant -- 6 degrees Celsius per kilometer simply serves as a ballpark reference for the lower troposphere

In light of the introduction to CAPE in the previous section, it should come as no surprise that the environmental lapse rate (which you can assess via 12Z or 00Z temperature soundings or by model forecasts) plays a key role in the calculation of CAPE. So when lapse rates are steep, (large decreases in temperature with altitude), CAPE tends to be high. CAPE, however, can also be relatively high when lapse rates are rather modest but the lower troposphere is moist. Indeed, the presence of low-level moisture tends to lower the LFC and increase CAPE accordingly.

Let's take a look at CAPE and lapse rates on a sounding to see what we can tell about the potential for strong updrafts and the stability of individual layers. For starters, check out the skew-T from Miami, Florida, at 00Z on July 9, 2010 (below)

The 00Z sounding at Miami, Florida, on July 9, 2010. The vertical profiles of temperature and dew point are the red and green soundings, respectively. The blue curve represents the path of an air parcel lifted from the surface. This sounding contained a "tall, skinny" area of CAPE (equal to 1,649 Joules per kilogram), and very little CIN.

Credit: College of DuPage

On this skew-T, the vertical profiles of temperature and dew point are the red and green soundings, respectively. The blue curve represents the path of an air parcel lifted from the surface. At the time, there was very little CIN and a CAPE value of 1,649 Joules per kilogram. Note that the temperature profile is dry adiabatic in the boundary layer (from the surface to about 930 mb), which represents a steep lapse rate. But, above that, the temperature profile is actually rather stable in most layers. One exception is the layer between roughly 930 mb and 800 mb, where the temperature profile is conditionally unstable, meaning that the environmental lapse rate is less than the dry adiabatic lapse rate but greater than the moist adiabatic lapse rate.

If you nudge a test parcel originating in this layer upward, its stability depends on whether or not the parcel is saturated (that's the "condition" of the instability). If the parcel is initially saturated and nudged upward from its initial position, it will accelerate away from its initial position because the parcel cools at the moist adiabatic lapse rate (keeping it warmer than the environment). However, if the parcel is unsaturated, it will quickly become cooler than its surroundings (and negatively buoyant) if nudged upward, because it cools at the dry adiabatic lapse rate. An unsaturated parcel would sink back to its initial position.

With the exception of another notable conditionally unstable layer from roughly 600 mb to 520 mb, most other layers above 800 mb are rather stable (small lapse rates).  Parcels originating in those layers will sink back to their original positions if nudged upward. So, where does all the CAPE (and potential for strong updrafts) come from? High surface temperatures (and steep lapse rates in the boundary layer), and high dew points in the boundary layer. If you look at the vertical profile of dew points in the boundary layer over Miami at this time, they varied from the upper 60s to the lower 70s degrees Fahrenheit (roughly 20 to 23 degrees Celsius). Yes, the boundary layer was rather moist. As a result, the LFC lay at a relatively low altitude, paving the way for a "tall, skinny" area of CAPE. The fact that lapse rates were relatively small above 800 mb made for relatively small differences a rising parcel's temperature and its surroundings, and a "skinny" positive area. In case you're curious, there were no thunderstorms around Miami at this time, despite the presence of CAPE and the very small amount of CIN present. For more discussion about why, check out the Explore Further section below.

CAPE resulting from steep lapse rates, creates stronger vertical accelerations and updraft velocities, and tends to catch forecasters' attention. Therefore, forecasters find it convenient to have options that allow them to take "shortcuts" and narrow their focus to areas where relatively high CAPE is primarily a result of steep lapse rates (where deep, moist convection tends to be more active, assuming, of course, that there's also ample moisture). As it turns out, so can you!

Consider the lapse rate products available on the SPC Mesoanalysis Page (in the "Thermodynamics" menu). Although the depths of thunderstorms (cloud base to cloud top) vary, forecasters typically look at low-level lapse rates (between the surface and three kilometers), and/or mid-level lapse rates (700-500 mb, or roughly 3-6 kilometers), depending on the local environment in which storms are expected to develop. Below is an example of an analysis of lapse rates, expressed in degrees Celsius per kilometer, in the 700-mb to 500-mb layer at 20Z on July 3, 2010.

Mid-level lapse rates (between 700 mb and 500 mb), expressed in degrees Celsius per kilometer, at 20Z on July 3, 2010, over the Northern Plains sector on SPC's Mesoanalysis Web page. Note the tongue of steep lapse rates that extended over western Nebraska into southwest South Dakota.

Credit: Storm Prediction Center

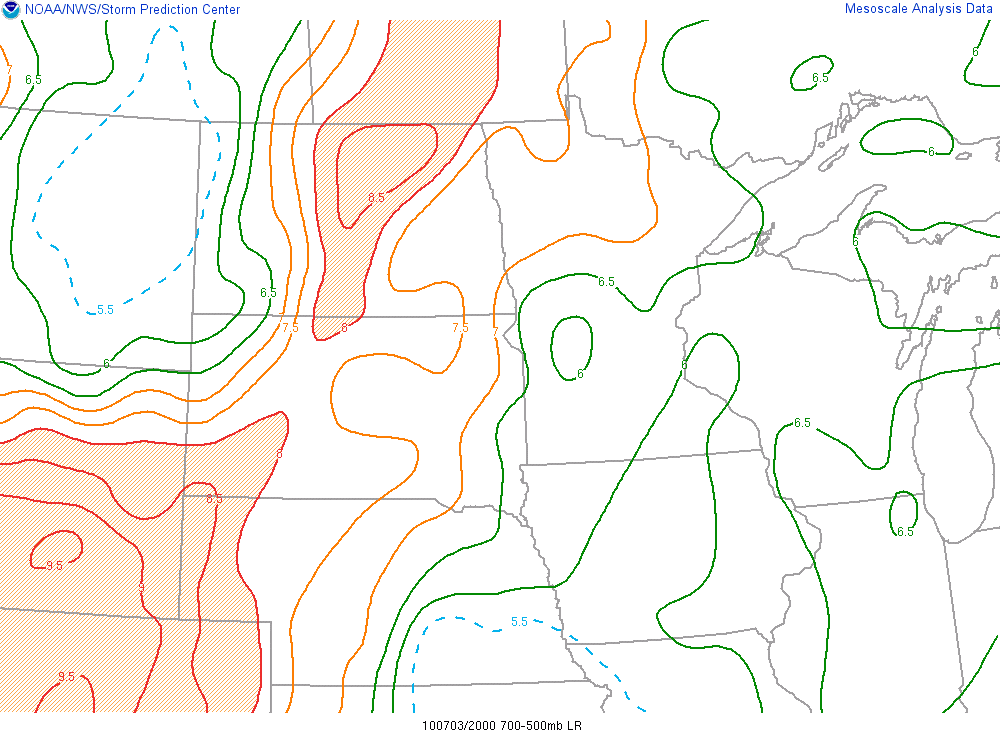
In the image above, note the tongue of very steep mid-level lapse rates extending northeastward across western Nebraska and southwest South Dakota (areas with lapse rates greater than 8 degrees Celsius per kilometer are shaded). These lapse rates were technically conditionally unstable since they were greater than the moist adiabatic lapse rate, but weren't quite as great as the dry adiabatic lapse rate. Still, in the real atmosphere, environmental lapse rates rarely exceed the dry adiabatic lapse rate, so you can consider lapse rates approaching 8 and 9 degrees Celsius per kilometer, as "steep" (generally favorable for deep, moist convection).

Low-level lapse rates (between the ground and three kilometers) were pretty steep over western Nebraska and southwest South Dakota, too (20Z low-level lapse rates). In turn, CAPE was also relatively high (20Z analysis of CAPE and CIN), and SBCIN (surface-based CIN) was vanishing in response to surface heating (note surface temperatures well into the 80s on the 20Z analysis of surface temperatures).

In this case, thunderstorms did erupt thanks to convergence associated with an approaching cold front (21Z surface analysis) and some rather weak upslope flow (topographic map). Both of these lifting mechanisms helped parcels overcome the remaining CIN to reach the LFC, setting the stage for thunderstorms (23Z radar reflectivity).

The moral of the story is that you should routinely look at lapse rates (both low- and mid-level) in situations where deep, moist convection might develop. And, as you'll see in the coming sections, analyzing the synoptic-scale pattern helps weather forecasters understand lapse-rate tendency (change in lapse rate over time), which helps forecasters anticipate potential changes to CAPE and CIN.

After identifying regions with relatively high CAPE and steep lapse rates and assessing whether synoptic-scale lift (or mesoscale lift) can get air parcels to the LFC, forecasters turn to the issue of vertical wind shear, which helps me to determine the mode of deep, moist convection. Let's investigate.

Read...

Of all the concepts you'll learn in this course, none has more forecasting utility than the following principle: Vertical wind shear governs the mode (type) of thunderstorms. Thus, vertical wind shear is of huge interest to mesoscale forecasters. After assessing the background synoptic-scale pattern and evaluating CAPE (and CIN) in order to identify regions where thunderstorms will likely be initiated, forecasters routinely turn their attention to vertical wind shear to help them assess what potential types of thunderstorms will develop, and how long-lived they might be. We haven't covered any details yet, but you've already heard me mention that long-lived, rotating updrafts usually form in environments with relatively strong vertical wind shear.

To get an understanding of the importance of vertical wind shear, we need to first learn how to determine vertical wind shear over a fixed point. Then I'll introduce and discuss Rapid Refresh analyses of vertical wind shear between the ground and an altitude of six kilometers, which, as you will also learn in this section, is a crucial layer that forecasters consider whenever supercells are possible.

For starters, as I've mentioned, vertical wind shear is a change in wind speed and/or wind direction with altitude. To get your quantitative bearings, check out this vertical profile of winds, showing an environment with relatively strong vertical wind shear between the ground and six kilometers. Note that wind direction doesn't change very much in the layer, but the dramatic increase in wind speed with height should be obvious. Now, compare the example with strong vertical shear to a vertical profile of winds with weak shear.

So, how do we formally calculate vertical wind shear? Given that the wind is a vector (it has both direction and magnitude), we can calculate vertical wind shear in any given layer of air by taking the wind vector at the top of the layer minus the wind vector at the bottom of the layer (vector subtraction).

Right off the bat, you should see that vertical wind shear is also a vector (the difference between two vectors is a vector). As a vector, vertical wind shear has both magnitude and direction. I realize that many of you aren't accustomed to working with vectors, but we can simplify the vector subtraction by plotting the wind vectors as shown below.

The black arrow represents the magnitude (in knots) and direction (314 degrees) of the wind shear vector in a given layer of air. The green vector indicates a wind at the bottom of the layer blowing from the southwest (250 degrees) at 10 knots. The blue vector represents the wind at the top of the layer blowing from the northwest (300 degrees) at 40 knots.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

On the graph above (called a "polar coordinate" graph), the circles represent wind speed expressed in knots and the interval between successive circles is 10 knots. The horizontal and vertical axes serve as references for a wind compass so that we can also take wind direction into account.

To start, let's assume that we want to calculate the vertical wind shear vector in a layer of air where the wind at the top of the layer blows from the west-northwest (300 degrees) at 40 knots, while the wind at the bottom of the layer blows from the west-southwest (250 degrees) at 10 knots. To plot the wind vector at the top of the layer, I estimated 300 degrees on the wind compass and judiciously placed a small dot (not shown) on the fourth concentric circle from the origin. Then I drew the vector corresponding to the wind at the top of the layer (bluish) from the origin to the dot. Now for the wind at the bottom of the layer. I estimated 250 degrees on the wind compass and placed a dot (not shown) on the innermost circle and drew the vector (in green).

To subtract the lower wind vector from the upper wind vector, simply draw a vector from the arrowhead of the lower wind vector to the arrowhead of the upper wind vector. Yes, the black vector represents the vertical wind shear vector in the layer. It has magnitude (35 knots) and direction (314 degrees). I'll spare you the trigonometry of how I arrived at that specific numerical answer, but you can at least see how the process works graphically. I also recommend checking out this interactive tool that automatically calculates the vertical wind shear vector for any given layer of air. Exploring this tool will allow you get comfortable with treating vertical wind shear as a vector.

Now that you have an idea of how vertical wind shear is calculated, the big question becomes, "What layer (or layers) of the troposphere is (are) important for predicting whether there will be long-lived, rotating updrafts?"

Cloud-Layer Shear

The answer to the question I just posed is vertical wind shear in the "cloud layer" (the layer encompassing the convective clouds that comprise thunderstorms). For the record, cloud-layer shear is simply the magnitude of the vector difference between the wind at cloud base and the wind at the top of the storm. A couple of aspects of shear within the cloud layer are critically important for thunderstorm forecasting. First, updrafts can be persistent (last longer) when deep-layer wind shear is sufficiently strong. Second, updrafts can begin to rotate (supercells can form) when low-level wind shear is sufficiently strong.

However, the altitudes of cloud bases and cloud tops (particularly the latter) vary from place to place and time to time. For example, the photograph below shows a high-based thunderstorm, which gets its name from a relatively high LCL. Not surprisingly, the depths of storms also vary with location (higher tops in southern Florida compared to southern Canada, for example) and with season (higher tops in summer, for example). Storm depths vary with the synoptic-scale environment as well (no surprise there, either). So, performing an exact cloud-layer shear calculation is quite challenging.

A relatively high-based thunderstorm over the lofty Cascade Mountains in the state of Washington during August 2007. Bases of thunderstorms are generally lower over humid regions such as the Gulf Coast States.

Credit: Krzysztof Z. Gajos

Given the challenges that exist in calculating cloud-layer shear exactly, how do forecasters approach the issue of vertical wind shear when it comes to forecasting deep, moist convection? In order to compare cases from one day to another, or from location to location, forecasters rely on the vertical wind shear between the ground and six kilometers (usually abbreviated 0-6 km shear or sfc-6 km shear) as a standard tool. Of course, 0-6km shear isn't really the same thing as cloud-layer shear, but forecasters often use it as a proxy when thunderstorm updrafts will be surface based (you'll learn later in the lesson that some thunderstorm updrafts don't actually originate at the surface).

Why 0-6 kilometers? Good question! As it turns out, model simulations conducted by the Weisman and Klemp in the 1980s helped to identify the layer between the ground and an altitude near six kilometers as pivotal for predicting thunderstorm type. If you're interested, here's Weisman and Klemp's classic 1982 paper. Although much of this paper is beyond what we've covered so far, by the end of the course, you'll actually be able to comprehend much of Weisman and Klemp's findings! Weisman and Klemp's simulations indicated that thunderstorms tended to be short-lived whenever model environments lacked deep vertical wind shear (strong shear didn't extend to altitudes near six kilometers). Later empirical research confirmed that vertical shear needs to be relatively strong through the lowest five or six kilometers of the troposphere in order for supercells to form.

With that background out of the way, let's take a quick look at an example. On June 5, 2009, the VORTEX2 team intercepted a supercell tornado in Goshen County in southeast Wyoming (YouTube video). At 22Z, the magnitude of the roughly westerly vertical wind shear between the ground and six kilometers was approximately 50 knots (see 22Z analysis below from the national archive at the Storm Prediction Center -- images of sfc-6 km Shear are listed as "shr6"). In real time, you can access regional fields of 0-6 km shear on SPC's Mesoanalysis page (in the "Wind Shear" menu).

The 22Z analysis of vertical wind shear between the earth's surface and an altitude of six kilometers on June 5, 2009.

Credit: Storm Prediction Center

The 50-knot shear magnitude between the surface and six kilometers over Wyoming is a "bulk" shear value, meaning that it's the overall shear between the top and bottom of the layer. Such "bulk" shear calculations do not account for "internal" changes in wind speed and / or direction that occur at intermediate altitudes between the ground and six kilometers. According to the Storm Prediction Center, the threshold of sfc-6 km shear that favors sustained, persistent updrafts (and possibly supercells) is roughly 35-40 knots, so the shear over southeast Wyoming at this time was plenty strong.

However, you shouldn't think of this 35-40 knot threshold for sustained updrafts and supercells as a "hard" threshold. Indeed, persistent updrafts and supercells can sometimes happen with lower magnitudes of 0-6 km shear. Given the right environmental conditions, some experienced forecasters start to consider the possibility of supercells when 0-6 km shear reaches about 20 knots, especially when there was a fairly dramatic change in wind direction between the ground and six kilometers (from the southeast near the surface to westerly or even northwesterly at six kilometers, for example). You will learn later that a dramatic turning of winds (change in wind direction) in the lower troposphere is an important ingredient that favors rotating updrafts.

There's no doubt that a magnitude of 20 knots for 0-6 km shear is way, way below the thresholds you'll see quoted by most sources, but at least thinking about the possibility of supercells in such environments helps to reduce the element of surprise from rare, "unexpected" supercells. The bottom line is that the probability of sustained, rotating updrafts increases markedly near the 35-40 knots quoted by SPC.  Therefore, I strongly recommend that you use this more-accepted threshold (35-40 knots) as we move through the rest of the course.

The upshot of this discussion is a basic rule you can take with you: All other factors being equal, the greater the 0-6 km shear, the greater the probability for sustained, rotating storms, especially when there's a dramatic change in wind direction from the ground to six kilometers.

Of course, 0-6 km wind shear doesn't stay "static" in time. It's constantly evolving depending on the synoptic-scale pattern, and those changes are a big forecasting consideration. Now that we've established the importance of variables like CAPE/CIN, environmental lapse rates, and 0-6 km shear, we'll shift gears to look at how the synoptic-scale pattern impacts these fields. Before we move on, however, keep in mind that vertical wind shear isn't just an issue in thunderstorm forecasting. Indeed, interested students may want to check out the Explore Further section below to see how vertical wind shear played a role in a national tragedy.

Read...

When forecasters assess the "big picture" in making a forecast, it's important to assess conditions throughout the entire troposphere. Therefore, forecasters frequently look at surface conditions (and forecasts), as well as those at 850 mb, 700 mb, 500 mb, and either 300 mb or 250 mb. Seasoned forecasters know what signs to look for at each of these levels as they relate to the possibility of deep, moist convection developing.

To get started, we're going to look at 500 mb, a level that you examined extensively in your previous studies. You should be very familiar with the features we'll be focusing on (namely, shortwave troughs), but now we're going to tie some of your past knowledge in with how these features can effect the environment for deep, moist convection. As you are about to see, shortwave troughs have important impacts on vertical motion and lapse rates that can make the environment more favorable for deep, moist convection.

Impacts of 500-mb Shortwave Troughs

For surface-based thunderstorms, synoptic-scale lift typically boils down to low-level convergence (along surface fronts and mesoscale boundaries) and upper-level divergence. Of course, there are other forms and scales of lift that can get air parcels to the LFC (orographic lift, for example). Here, however, I only want to address synoptic-scale lift in this section, and, in particular, divergence downwind (usually east or northeast) of a 500-mb trough. For starters, review this animation tracking a parcel through a shortwave trough, which I hope you recall from your previous studies. The schematic below serves as a supplement for the animation. Any way you slice it, there's divergence downwind of a 500-mb shortwave trough because air parcels moving east from the base of a shortwave trough lose some of their spin (absolute vorticity decreases) by expanding their surface areas. Sound familiar? This upper-level divergence, in concert with low-level convergence, encourages upward motion, which promotes local cooling.

A shortwave ridge and trough at 500 mb. The thin, dark contours represent 500-mb heights, and the dashed, red contours are isovorts (isopleths of absolute vorticity). The checkered cylinder represents a parcel of air, which we assume travels through the shortwave ridge and trough. Note that as the parcel travels east of the shortwave trough, it's spin decreases as its surface area increases. This increase in surface area is consistent with mass divergence east of the shortwave trough.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

Of course, the animation and schematic above are highly idealized. Shortwave troughs often don't look as neat and tidy as they do in these idealized graphics. Take, for example, the 500-mb pattern shown by the 12Z run of the NAM on February 2, 2016, valid at 18Z that day. The feature that probably jumps out at you right away is the closed low and strong vort max right over the center of the country. That closed low marks the core of a longwave trough, but embedded within that longwave trough are several shortwave troughs.

A couple of those shortwave troughs are marked by the X's over northern Mexico. But, there's another shortwave trough over New Mexico that is not marked by an X. Do you see it? The very small closed contour (darker yellow shading) over Central New Mexico also marks a subtle vort max and shortwave trough, even though it lacks the classic "X." The details of the positions and intensity of shortwave troughs (even subtle ones) is of great interest to mesoscale forecasters, because those details determine where (and how strong) the divergence is.

To get an idea of what I'm talking about, check out this 17Z Rapid Refresh analysis of 500-mb heights (black contours), vorticity (dashed contours and color-filled regions), and differential vorticity advection (blue contours) from February 2, 2016 (one hour before the NAM forecast prog above was valid). You can think of differential vorticity advection as a proxy for upper-level divergence. Note that the strongest divergence is located in a band from eastern Nebraska through Iowa and into Illinois, to the northeast of the strongest vort max (over Kansas). However, there are lots of other pockets of differential vorticity advection (divergence) over the Southern Plains due to the details of the vorticity field. Note that our subtle vort max over New Mexico was creating some weak divergence just to its east, as well.

On this particular date, SPC had outlined an enhanced risk of severe weather in their Day 1 Convective outlook, but the greatest risk area wasn't related to the strongest divergence at 500 mb. It was farther south, in the path of those more subtle vort maxes, where periods of weaker divergence aloft would occur throughout the day as those weaker vort maxes rounded the base of the longwave trough as it crawled eastward. In other words, the severe weather threat isn't always where the strongest lifting at 500-mb is!

So, why is synoptic-scale lifting and its associated cooling pivotal to the development of deep, moist convection? It reduces (or removes) CIN! For starters, a typical vertical profile of temperature associated with the presence of CIN often shows a stable layer in the lower troposphere (on the interactive tool below, note the stable layer just above 850 mb). You may think of this stable layer as relatively warm air. To see what I mean, recall that, within a stable layer, temperature sometimes increases with increasing altitude (a temperature inversion), stays constant with increasing altitude (an isothermal layer), or decreases rather slowly with height. If you look closely at the idealized sounding, the stable layer just above 850 mb is helping to create CIN (shaded in pink).

Now, let's follow the evolution of the stable layer (a weak inversion, in this case) as a 500-mb shortwave trough approaches. Remember, there's upper-level divergence east of the 500-mb shortwave. Assuming a surface boundary also lies to the east of the 500-mb shortwave (which is a reasonable assumption), then there's also some low-level convergence to help the cause. At any rate, there's upward motion and cooling in local columns of air that extend up to 500 mb on the eastern flank of the 500-mb shortwave. To simulate this lifting and cooling, drag the shaded layer of air upward in the tool above.

Above the well-mixed boundary layer, the temperature sounding shifts to the left (the air cools aloft) in response to the upward motion associated with divergence ahead of an approaching 500-mb shortwave trough, which reduces CIN and lowers the altitude of the LFC.

What happens to CAPE when there's cooling from upward motion? To focus solely on this process, we assume that the surface temperature and dew point hold steady. The leftward shift of the temperature sounding above the boundary layer means that CAPE also increases (positive area increases). When you look at the temperature sounding at lower altitudes, note that the depth of the well-mixed boundary layer increases with time. That's because cooling (via upward motion) at the top of the boundary layer promotes local mixing so that the depth of the well-mixed layer expands.

The bottom line is that synoptic-scale lift reduces CIN, and increases CAPE. So, as a developing mesoscale forecaster, you should think of divergence east of a 500-mb shortwave trough as a way to "prime" the troposphere for deep-most convection. Indeed, a 500-mb shortwave does not really "trigger" thunderstorms. It simply makes the environment more conducive for thunderstorms to develop because it helps to reduce CIN.

Height Tendencies and Lapse Rates

Upward motion, however, isn't the only way that 500-mb shortwave troughs can make the environment more favorable for thunderstorms. In addition, falling 500-mb heights ahead of the shortwave trough tend to go along with decreasing mid-tropospheric temperatures (recall that the cores of 500-mb closed lows and shortwave troughs are mid-level pockets of relatively cold air). In other words, cooling at 500 mb usually helps to destabilize the middle troposphere. A 500-mb shortwave trough tends to cause mid-level lapse rates to increase with time (the lapse-rate tendency is positive).

As we get even closer to the core of an open 500-mb shortwave trough (or a closed low), 500-mb heights noticeably "fall" (decrease) over time as the system moves eastward, and mid-level lapse rates steepen even further. To see an example, check out the image below showing 500-mb heights (black contours) at 21Z on July 14, 2010, and the 12-hour height tendencies leading up to that time. Treating 500-mb lows and troughs as mid-level pockets of cold air, it stands to reason that 500-mb temperatures typically decrease as these cold pockets approach. Assuming there's some solar heating and / or some low-level convergence to get surface air parcels to the LFC, showers and thunderstorms can also develop closer to the core of the 500-mb low or open trough.

500-mb heights at 21Z (black contours), and the 12-hour 500-mb height changes at 21Z on July 14, 2010 (from 09Z to 21Z). The dashed-blue contours represent height falls in meters (blue-filled areas represent the largest height falls). Dashed-red contours indicate height rises in meters (red-filled areas represent the largest height rises). Note the large height falls in south-central Canada, North Dakota, and Minnesota (ahead of the closed 500-mb low and its associated trough).

Credit: Storm Prediction Center

Note the pocket of height falls to the east of the 500-mb shortwave trough centered near the Saskatchewan / Manitoba border at 21Z. In the 12 hours leading up to 21Z, heights had been falling (and mid-level lapse rates increasing) out ahead of the trough, with the biggest height falls marked by the blue shaded region just southeast of the closed low.

The mid-level cooling and steepening lapse rates associated with 500-mb troughs acts to boost CAPE values, favoring stronger updrafts as long as parcels are able to reach the LFC. So, 500-mb troughs can prime the atmosphere for deep, moist convection through reducing CIN via synoptic-scale upward motion, and through boosting CAPE from mid-level cooling. To see all of these processes in action, check out the Case Study video below.

Mid-Level Jets

Impacts on CAPE, CIN, and lapse rates aren't all forecasters think about when they evaluate the 500-mb pattern. They also look for "mid-level jets" (zones of fast winds at 500 mb). For example, the 12Z 500-mb RUC analysis from July 14, 2010 (same date as the height tendency map above) shows a 500-mb speed maximum over the Upper Middle West that shadowed the vigorous shortwave trough.

Why are mid-level jets like this one important? They tend increase the vertical wind shear in the layer from the ground to six kilometers. Remember that the 500-mb level tends to be around 5,500 meters, so when relatively fast winds exist around that level, vertical wind shear tends to increase in the layer between the surface and six kilometers. Regardless of any changes in wind direction, the fast flow in the middle troposphere that goes along with a mid-level jet means there is usually a marked increase in wind speed between the surface (where friction slows the wind speed) and the middle troposphere.

Now that you've seen how 500-mb shortwave troughs can prime the atmosphere for deep, moist convection, and mid-level jets (which sometimes exist in concert with 500-mb shortwaves), please take some time to view the Case Study below, which details how the arrival of the 500-mb shortwave trough and mid-level jet that you just saw helped to spur deep, moist convection (and severe weather) over the Upper-Mississippi Valley.

Read...

The upper-air pattern is critically important to mesoscale forecasters for a number of reasons, some of which you already saw in our discussion of the big picture at 500 mb. Another reason that the upper-level pattern is important is that it can affect where surface boundaries develop. One such way this can happen is with the development of "lee troughs."

When strong westerly winds blow across the Rockies, a trough typically forms in the lee of the mountains (the side facing away from the wind, where winds blow down the slope) over the western high plains. For the record, similar troughs can form sometimes in the lee of the Appalachians and other smaller mountain ranges, too. These troughs are called lee troughs because of the location where they develop. The 700-mb chart at 12Z on January 1, 2004 (right image below), shows a classic height pattern consistent with fairly strong southwesterly winds that set the stage for a lee trough to form (note the trough that is evident east of the Rockies).

(Left) The Rocky Mountains (high resolution). (Right) The 700-mb analysis at 12Z on January 1, 2004, shows a classic height pattern consistent with fairly strong southwesterly winds and the formation of a lee trough east of the Rockies.

Credit: Earth System Research Laboratory

How does a lee trough form east of the Rockies (and, to a lesser extent, east of the shorter Appalachians)? In your previous studies, you learned about absolute vorticity, which we expressed as z + f (relative vorticity plus planetary vorticity). Monitoring the change in an air parcel's 500-mb absolute vorticity with time and linking to mass convergence or divergence indicates that absolute vorticity is not a "conserved" property. In other words, an air parcel's 500-mb vorticity changes in time -- it's not constant, or "conserved." We're in luck, however, because Ertel's Potential Vorticity is a conservative property for relatively large-scale motions in the atmosphere. Mathematically,

The conservation of Ertel's potential vorticity involves the give-and-take between relative vorticity, the Coriolis parameter and the height of an air parcel or air column.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

where z is relative vorticity, f is planetary vorticity, (z + f)/H is Ertel's Potential Vorticity and H is the height of an air parcel (or air column). The above equation asserts that the ratio of an air parcel's (or air column's) absolute vorticity to its height is always conserved.

Conceptually, this relationship should make sense to you, as visualized in this animation of a parcel with a changing rate of spin. A parcel (or column) that spins faster (has greater absolute vorticity) must also get taller as convergence occurs (remember that mass and angular momentum are also conserved). Meanwhile, a parcel (or column) that spins slower (less absolute vorticity) must get shorter as divergence occurs.

Therefore, assuming the absolute vorticity of an air column is positive (cyclonic), any stretching in the vertical results in an increase in cyclonic spin (in other words, an increase in absolute vorticity). Let's see if we can apply this idea to the interaction between westerlies and mountains in the mid-latitudes to see how a lee trough forms.

Suppose a column of air extending from the ground to the tropopause moves directly eastward toward the Rockies (see below). Further assume that its relative vorticity is zero (no shear or curvature) and that the planetary vorticity is 10 x 10^-5 seconds^-1. With these assumptions in mind, let's follow the air column up a mountain (as illustrated by the chalkboard diagram below). Clearly, H starts to decrease since the distance from the surface to the top of the troposphere is smaller on top of the mountain.

Assuming a westerly wind, an eastward-moving air column (parcel) ascending the windward slopes of the Rockies must make an anticyclonic turn in order to conserve Ertel's Potential Vorticity. After reaching the summit and descending the lee side of the mountains, the column's relative vorticity must increase to offset the increasing H and the decreasing f. Thus, the column transitions to a cyclonic turn, forming a lee trough east of the Rockies.

Click for a text description.

Formation of a Lee Trough

Assume that a parcel is traveling in a straight path with zero relative vorticity but having positive absolute vorticity (due only to $f$).

As the parcel encounters the mountain, $H$ decreases. Therefore, $\zeta$ decreases, causing the parcel to follow an anticyclonic path.

As the parcel travels south, $f$ decreases, causing an increase in $\zeta$. The increase in $\zeta$ results in a cyclonic curvature to develop.

As the parcel travels away from the mountain, $\zeta$ is further increased by an increase in $H$. At this point, the parcel's trajectory is very cyclonic, thus forming the base of the lee trough.

As $\zeta$ decreases to zero, because of an increasing $f$, the parcel's trajectory contains less and less curvature.

The large cyclonic curvature causes the parcel to turn northward, increasing $f$. The increase in $f$ dictates a corresponding decrease in $\zeta$.

Equation:

$$\frac{\zeta + \mathit{f} }{\mathit{H}}= \text{ constant }$$

A small schematic at the bottom illustrates airflow over a mountain, represented with wavy lines. Cylinders with spirals show the airflow patterns and vorticity.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

In order to conserve Ertel's Potential Vorticity, the column makes an anticyclonic turn and heads southward. Why southward? First, both z (relative vorticity) and f (planetary vorticity) must decrease in order to offset the decrease in H. Recall that the initial relative vorticity was zero, so a decrease in z translates to negative (anticyclonic) relative vorticity. Okay, once the column reaches the summit and starts to descend the lee slopes, H increases (the column stretches vertically). The only way to offset this increase in H is for the relative vorticity of the southward-moving column (toward lower values of planetary vorticity) to increase. Thus, the column starts a cyclonic turn, gradually tracing out a trough east of the Rockies. This cyclonic turn is consistent with the vertical stretching and column spin-up that I discussed earlier.

Once the air parcel completes the cyclonic turn and heads northward, relative vorticity will start to decrease to offset the increase in f (remember, planetary vorticity increases with increasing latitude). The parcel will eventually start an anticyclonic turn that will cause it to move in a southward direction. In essence, steady westerly flow over the Rockies results in a lee trough east of the mountains and then an dampening series of wave-like motions farther east. The presence of an upper-air trough in the lee of the mountain range can make the region ripe for cyclogenesis.

But, lee troughs aren't just an upper-air feature. After parcels in the fast southwesterly flow pass the crest of the Rockies, they blow down the slopes of the eastern side of the Rockies and warm via compression. That warming lowers the density of local air columns, resulting in the formation of a surface trough of low pressure. For example, note surface trough at 12Z on January 1, 2004 (the same time as the 700-mb map above).

Given the surface lee trough that forms as well, in response to the warming of downsloping air columns via compression, lee troughs create a zone of surface convergence. But, that's not the whole story with respect to their impact on surface weather. Lee troughs can also help draw moist air northward from the Gulf of Mexico as wind flow in the lower troposphere turns more southerly ahead of the trough. Indeed, lee troughs can aid in the formation of dry lines (recall that dry lines are boundaries between moist and dry air). For example, the strong southwesterly flow aloft over the southern Rockies, as seen on this 700-mb analysis from 12Z on June 10, 2004, resulted in the formation of a lee trough. Within the lee trough that developed along the Texas / New Mexico border, a dry line developed (check out the 12Z surface weather map from the date) as moist air from the Gulf of Mexico accelerated northward east of the trough, increasing dew-point gradients and thereby helping to create the dry line.

Increased low-level moisture (higher dew points) acts to reduce CIN, as you've learned, which can make the environment more favorable for thunderstorm development. So, there's no doubt that forecasters want to keep their eye on the formation of lee troughs! We'll certainly encounter them again. With this background out of the way, let's turn our attention more generally to surface boundaries and the roles that they play in initiating deep, moist convection. Read on.

Read...

When I evaluate the lower troposphere for its potential to initiate and support deep, moist convection, I routinely look at several fields, including surface temperatures and dew points (as well as their profiles in the first several thousand feet above the ground). After deciding that the overall thermodynamic environment favors an outbreak of thunderstorms based on relatively high CAPE and low CIN, I then search for surface boundaries. I'm using "surface boundaries" here as a generic "catch-all" term for fronts and mesoscale boundaries such as dry lines, sea-breeze fronts, and outflow boundaries (we'll explore these features in more depth later). My forecasting checklist includes this search because surface boundaries have the potential to lift air parcels to the LFC.

As you already know, low-level lift is often associated with surface convergence (orographic lift can also get air parcels to the LFC). Ultimately, identifying surface boundaries that have the potential to lift air parcels to the LFC boils down to finding areas where there's low-level convergence. Not surprisingly, there are a couple of important tools that help forecasters to detect low-level convergence, and they're the focus of this section.

WPC Analyses, Satellite and Radar Imagery

Where should you start your search for surface boundaries? The surface analyses from the Weather Prediction Center (WPC) are a good place to start. On the most fundamental level, identifying surface fronts should always be a top priority because they can help to lift air parcels to the level of free convection. There's a broader, more philosophical reason, however, for you to sit up and take notice of surface fronts. There's a crusty, old forecasting rule that most severe thunderstorms occur in the warm sector of a mid-latitude low (the region ahead of the low's cold front and on the warm side of the warm front), or on the cool side of a warm or stationary front within 300 kilometers of the front.

This "old school" law of forecasting is probably one of the most important you'll encounter in this course because it can really help you keep your bearings when assessing potential areas for severe weather outbreaks. It won't help you catch every single area at risk for severe thunderstorms, but it will help you find most of them (especially the "big" outbreaks).

Either way, surface boundaries (fronts, troughs, dry lines, outflow boundaries, etc.) are certainly something to keep your eye on because they are typically zones of low-level convergence. However, surface boundaries typically don't initiate storms everywhere. So, at face value, WPC surface analyses don't always show exactly where the surface boundaries are going to be "active." Therefore, we need some additional help in identifying where thunderstorms may erupt along a surface boundary. For assistance, we'll turn to our indispensable old friends, satellite and radar imagery.

Let's use May 10, 2011 as an example. The 21Z surface analysis on May 10, 2011 (illustrated below), showed a dry line and a series of fronts over the Middle West that were associated with an occluding low-pressure system over North Dakota. Were any of these surface boundaries about to initiate thunderstorms? To answer this question, let's turn to satellite and radar imagery.

The 21Z surface analysis on May 10, 2011.

Credit: Weather Prediction Center

On the 21Z analysis above, turn your attention to the long dry line that weaved its way from Texas all the way to the southern border of Minnesota on the map. But, a look at satellite imagery shows that the boundary likely didn't stop there. If you look at the 1945Z visible satellite image, you'll see a boundary between clear air and a cumulus field over Minnesota, which likely was the northern portion of the dry line. WPC elected not to analyze it probably because there weren't enough station models to detect the dry line in that area. At 21Z, the stationary front over western Minnesota clearly lay west of the surface boundary represented on satellite imagery (compare the 21Z visible image to a close-up 21Z surface analysis). At any rate, this portion of the dry line started to initiate thunderstorms by 21Z, and a few hours later, some nasty-looking storms were underway (2245Z visible image).

Radar imagery also suggested the presence of this surface boundary over Minnesota. The 21Z composite of base reflectivity showed a line of generally weak reflectivity representing insects, etc. caught in the pattern of low-level convergence associated with this portion of the dry line. Just two hours later, the 23Z composite of base reflectivity shows deep, moist convection initiating along the boundary.

The moral of this story is that while synoptic-scale surface analyses are helpful in identifying large-scale surface boundaries, satellite and radar imagery are critical forecast tools that can point the way to where thunderstorms may erupt along those boundaries (or other subtle boundaries not obvious from a surface analysis map).

There are other ways you can assess low-level convergence and its potential to initiate thunderstorms, and I'll discuss them now in the context of the outbreak of severe weather that occurred over the Upper Middle West on on July 14, 2010.

July 14, 2010

Previously, we explored the role that the 500-mb pattern played in priming the atmosphere for deep, moist convection in the Upper-Mississippi Valley on July 14, 2010 (you may want to revisit the video Case Study on that page). While the 500-mb pattern made the atmosphere generally more favorable for deep, moist convection, it was surface boundaries that determined the specific locations where thunderstorms would erupt. Now we're going to focus on the occluded and cold fronts in Minnesota, which you can see on the 21Z surface analysis. Low-level convergence along these boundaries helped lift parcels to the LFC, causing thunderstorms to erupt (check out the 21Z mosaic of composite reflectivity).

Anticipating the onset of severe thunderstorms, SPC forecasters issued a "Mesoscale Discussion," which they typically do when severe thunderstorms are slated to develop in the next several hours (read more about Mesoscale Discussions, if you're interested). In Mesoscale Discussion #1303, SPC forecasters mentioned the pivotal role of low-level convergence in the initiation of thunderstorms along these two fronts (excerpt below):

If you're confused by the mention of "DVPA," don't worry. It's just an acronym for "differential positive vorticity advection," which is a fancy proxy for divergence downwind of the vort max mentioned in the next sentence of the discussion. But, clearly, forecasters at SPC recognized the importance of the occluded and cold fronts in creating low-level convergence that could lift parcels to the LFC.

The 19Z analysis of surface streamlines. Note the area of surface convergence in Minnesota (within the white circle).

Credit: © Penn State is licensed under CC BY-NC-SA 4.0

As you learned previously, forecasters routinely examine charts of surface streamlines to pinpoint lines of low-level convergence. Indeed, the 19Z analysis on July 14, 2010 (above), revealed a line of surface convergence along the occluded and cold fronts in Minnesota; it was one of the key factors that prompted SPC forecasters to issue MD #1303. In a nutshell, the confluence or "coming together" of streamlines in the region corresponds to low-level convergence. Note that we can directly connect confluence to mass convergence at the surface, but not necessarily aloft, for reasons we'll discuss later.

With regard to initiating surface-based thunderstorms, it's important that the air converging along a surface boundary is relatively moist. As it turns out, there are actually two processes typically at work along surface boundaries that initiate deep, moist convection: low-level convergence and moist advection. For the record, moist advection is the horizontal transport of moist air by the wind.

One standard way to measure moisture, which you may remember from previous courses, is mixing ratio. As a reminder, mixing ratio is the ratio of the mass of water vapor to the mass of dry air in a parcel, and is usually expressed in grams per kilogram. Let's use mixing ratio to assess the air that converged along these boundaries to initiate thunderstorms on July 14, 2010. If you check out this analysis of 1000 mb streamlines (a proxy for the surface) superimposed on mixing ratio at 21Z, you can easily see the predominant southerly flow from the Gulf of Mexico that advected moisture far northward over the Upper Mississippi Valley. To get your bearings, the contour interval for mixing ratio is 2 g/kg, and values exceeding 18 g/kg are color-filled in green to indicate moist air. Note the "tongue" of high mixing ratios (very moist air) that extended into Minnesota and south-central Canada.

For convenience, SPC forecasters combine the two processes of low-level convergence and moist advection into a single field called moisture convergence. For the record, the magnitude of convergence in the calculation usually dominates the magnitude of advection, so this field gives forecasters a good proxy for surface convergence. The 21Z surface analysis of this field on July 14, 2010 (below), indicates relatively strong moisture convergence (solid red contours) in Minnesota near the secondary low and along the occluded and cold fronts. Note, just a tad farther east, that there's another pocket of moisture convergence. This pocket coincides with an area where discrete tornadic supercells erupted near eastern Minnesota and the western Wisconsin border. By now you should be getting the sense that moisture convergence near the ground goes hand in hand with initiating surface-based thunderstorms.

The 21Z analysis of moisture convergence (red contours) and surface mixing ratio. Thin, dark contours correspond to values of mixing ratio (the contour interval is 2 g/kg, and mixing ratios exceeding 16 g/kg are color-filled in dark green to indicate the areas that are very moist). Note the area of rather strong moisture convergence over Minnesota, where a secondary low, an occluded front, and a cold front were pressing eastward at this time. For the record, the units of moisture convergence are grams per kilogram per second.

Credit: Storm Prediction Center

These maps from SPC are really useful because they allow you to see surface winds, mixing ratios, and moisture convergence together. For mixing ratios, the contour interval is 2 g/kg and mixing ratios exceeding 16 g/kg are color-filled with dark green in order to indicate the areas that are quite moist. For the record, the units of moisture convergence are grams per kilogram per second. Those units might seem odd to you at first, but keeping in mind that the units of mixing ratio are grams per kilogram, the "per second" makes sense since we're measuring moist air coming together in time.

If you're interested in finding resources for assessing low-level convergence via streamlines and moisture convergence, check out the Explore Further section below, as it has some key data resources for you. Otherwise, up next, we're going to look at some "sneaky" ways that low-level convergence can help initiate thunderstorms. As it turns out, moisture convergence doesn't only occur along fronts. Let's investigate.

Read...

When you originally learned about the classic model of a mid-latitude cyclone, you learned that the model includes showers and thunderstorms developing along or just ahead of the low's cold front. As you just saw in the previous section, cold (or occluded) fronts serve as classic lines of low-level convergence that can lift parcels to the LFC, initiating thunderstorm formation. But, sometimes, lines of showers and thunderstorms form farther out ahead of cold fronts. Let's investigate.

Prefrontal Troughs

Check out the surface analysis at 06Z on February 11, 2009 (below). At the time, a cold front associated with a low centered over the panhandle of Texas was moving east across eastern Texas. Ahead of the cold front, a squall line had formed in a prefrontal trough, where low-level convergence played a role in getting air parcels to the LFC. For the record, a prefrontal trough is simply a trough (elongated area of low pressure) preceding a cold front that is usually associated with a wind shift. The storms on February 11, 2009 meant business (06Z composite of radar reflectivity), and SPC eventually issued a Tornado Watch as the squall line roared eastward.

The 06Z surface analysis on February 11, 2009, shows that a squall line had developed in a trough ahead of a cold front (a prefrontal trough).

Credit: Weather Prediction Center

To affirm the convergence in the surface trough (where the squall line formed), please note the confluence of the wind barbs (southerly just ahead of the trough and west-northwesterly and southwesterly just behind the trough). The corresponding 06Z analysis of surface streamlines leaves no doubt about confluence over eastern Texas along the prefrontal trough. At the surface, this confluence indicates convergence (remember, that's not necessarily true aloft), but can we get a little more quantitative with our assessment of low-level convergence?

Another useful tool for identifying regions where there might be sustained and "dependable" lines or areas of convergence in the boundary layer is SPC's deep moisture convergence (or "deep moist convergence") product. Sometimes, looking at moisture convergence right at the surface doesn't paint the clearest picture of where sustained, meaningful moisture convergence is occurring. So, SPC's deep moisture convergence product averages moisture convergence in the lowest two kilometers of the troposphere. In other words, if there's something happening in the boundary layer, this field usually shows it. Like moisture convergence at the surface (discussed in the previous section), the convergence term tends to dominate the advection term, so you can use this product as a proxy for convergence in the lower troposphere.

As a quick aside, SPC calls the product "Deep Moist Convergence", but I will use "deep moisture convergence." That's because "deep moist convergence" looks a lot like "deep, moist convection, and I don't want you to get these two terms mixed up (it's easy to do).

The 06Z analysis of deep moisture convergence on February 11, 2009 (below), shows that there was ample deep moisture convergence associated with the prefrontal trough over eastern Texas (the red contours represent lines of constant deep moisture convergence). For the record, the units of deep moisture convergence are grams per kilogram per second (the same as the units of surface moisture convergence).

The 06Z analysis of deep moisture convergence on February 11, 2009. Red contours indicate lines of constant deep moisture convergence (dashed contours represent lines of constant moisture divergence). Note the strong, deep moisture convergence associated with the prefrontal trough over eastern Texas. The thin, green contours are lines of constant mixing ratio in the lowest 100 mb of the troposphere.

Credit: Storm Prediction Center

Clearly, the confluence along the prefrontal trough corresponded to strong deep moisture convergence. In case you're wondering, 06Z field of surface moisture convergence was much less impressive, so there's often an advantage in assessing the deep moisture convergence to catch the impacts of moist advection and convergence throughout the boundary layer.

Now that we've seen that prefrontal troughs can be regions of deep moisture convergence, which can lift parcels to the LFC, what exactly causes prefrontal troughs? In many cases, it's the prevailing synoptic-scale pattern. For the case of the prefrontal trough over eastern Texas on February 11, 2009, synoptic-scale forcing was certainly the culprit. At the time, there was a closed 500-mb low trailing the cold front to the west. Farther to the east of the strong vort max associated with the 500-mb closed low, a lobe of vely high absolute vorticity likely produced enough upper-level divergence to promote surface pressure falls ahead of the cold front. Note that this analysis has isovorts contoured every 2 units instead of every 4 so that the lobe of relatively high vorticity was easier to pick out.

It's often subtle, weaker vort maxima like this one that can lead to surface pressure falls and prefrontal troughs. Of course, another potential cause of prefrontal troughs that you learned about previously is a lee trough, which can form over the Plains (or east of the Appalachians) with relatively fast westerly flow blowing over the mountains. If you're interested in learning more about the possible causes of prefrontal troughs, I recommend the paper "A Review of Cold Fronts with Prefrontal Troughs and Wind Shifts," published in Monthly Weather Review.

Regardless of the specific cause of a prefrontal trough, you should be much more concerned about the potential role a specific prefrontal trough might play in a subsequent outbreak of severe weather. Analyses of mean sea-level pressure, surface streamlines, and analyses of deep moisture convergence (or sometimes surface moisture convergence) will help you identify potential zones of confluence and convergence where parcels may be lifted to the LFC.

With that said, however, sometimes there's confluence that we need to be aware of without an obvious prefrontal trough (or clear surface trough of any type). On February 11, 2009, the prefrontal trough over eastern Texas (where the squall line formed) was pretty obvious on the 06Z synoptic-scale analysis of mean sea-level pressure. But, without such an obvious prefrontal trough, surface streamlines can still help forecasters identify confluent zones.

In such cases, one could argue that surface streamlines are even more useful than analyses of mean sea-level pressure because they cut right to the chase. In the grand scheme of forecasting, determining whether or not a trough happens to be coincident with a confluence of surface streamlines doesn't really matter. The fact that there's confluence and low-level convergence is what matters, and using surface streamlines will allow you to get a quick sense for where there's low-level convergence that has the potential to get air parcels to the LFC.

To highlight the utility of surface streamlines, check out the 21Z analysis of surface streamlines from February 18, 2009 (below):

The 21Z analysis of surface streamlines on February 18, 2009 shows a zone of weak confluence across Mississippi and Alabama. Note the "squeezing together" of streamlines in the oval.

Credit: Storm Prediction Center

A region of confluence was readily apparent across Mississippi and Alabama as southwesterly streamlines "squeezed together." Meanwhile, if we examine the corresponding 21Z surface analysis, is the region of confluence as obvious? Not really. At the time, much of the Southeast lay in the warm sector of a mid-latitude cyclone centered over Lake Huron, but at first glance, the warm sector looks rather commonplace, with no prefrontal troughs or apparent areas of surface convergence. So, a forecaster that just looked at the analysis of mean sea-level pressure may have easily missed this zone of confluence, which is why I highly recommend incorporating streamlines into your forecasting routine!

As it turned out, this rather weak confluence ahead of the cold front (in the warm sector) produced just enough surface convergence in the warm sector to get air parcels to the LFC and set the stage for discrete supercells to erupt (check out the 2330Z reflectivity). For the record, surface-based CAPE was relatively high in the warm sector, and the vertical wind shear was strong.

Deep Moisture Convergence and Thunderstorm Mode

Were you surprised to see that "rather weak confluence" helped to initiate discrete supercells, which represent some of the most violent thunderstorms on Earth? I confess that it might seem a bit contradictory at first. Allow me to shed a little light on what seems to be a paradox.

For starters, take a look at the 21Z analysis of deep moisture convergence on February 18, 2009 (shown below). To get your bearings, the red contours represent lines of constant deep moisture convergence, and the thin green contours indicate the average mixing ratio in the lowest 100 mb of the troposphere. The deep moisture convergence in the warm sector over the Southeast States (where supercells erupted) is generally weak and rather piecemeal (scattered or fragmented).

The 21Z analysis of deep moisture convergence on February 18, 2009. Please note that deep moisture convergence was rather weak and piecemeal in the warm sector over the Southeast States. Nonetheless, discrete supercells erupted over this region.

Credit: Storm Prediction Center

I realize that "weak" is somewhat of a subjective description, but with a comparison, I think you'll see why I classified it as weak. Compare the deep moisture convergence in the warm sector at 21Z on February 18 (above) with the deep moist convergence over the eastern Gulf and Southeast Coasts 12 hours later at 09Z on February 19. No contest, wouldn't you agree? The strong, organized band of deep moisture convergence along the Gulf and Southeast Coasts was associated with the strong cold front, which had obviously advanced southeastward during the 12-hour period after 21Z.

The transition to stronger, more organized deep moisture convergence translated to big differences in thunderstorm mode (type). At 2330Z, when the deep moisture convergence was weak and piecemeal, discrete supercells were able to erupt (2330Z radar review). But, with much stronger, more organized deep moisture convergence, a large, organized line of thunderstorms developed (0925Z radar, for comparison).

The bottom line here is that strong surface convergence distributed rather uniformly along a surface boundary tends to initiate large "thunderstorm systems" that are more organized (in this case, a long line at 09Z on February 19, 2009). Conversely, weak, piecemeal convergence (confluence) at the surface tends to initiate discrete storms. Not surprisingly, there's more to the story, and I'll fill in all the scientific details later in the course.

Now that you have a better sense for the role that the synoptic-scale surface pattern plays in the development of deep, moist convection, let's move our big-picture overview up to 850 mb. In the meantime, if you're interested in learning how to access analyses of deep moisture convergence, check out the Explore Further section below.

Read...

So far, we've covered the roles of the 500-mb pattern and surface convergence in the development of deep, moist convection. Now it's time to see what forecasters look for at another level in the lower troposphere--850 mb. What aspects of the 850-mb pattern provide clues for forecasters about the development of thunderstorms?

In short, forecasters are primarily looking for two things at 850 mb--evidence of warm advection and the presence of low-level jet streams (ribbons of relatively fast winds in the lower troposphere). Why are these things important to forecasters? Let's investigate, starting with 850-mb warm advection.

You learned in your previous studies that the strongest warm advection associated with a mid-latitude low-pressure system occurs along and north of the low's warm front (not in the warm sector, which tends to be relatively homogeneous with regard to temperature). You also learned that warm advection north of a warm front goes hand in hand with overrunning. Thus, the footprint of overrunning at 850 mb is, not surprisingly, a pocket of warm advection. Below, the 14Z 850-mb analysis on July 14, 2010, shows that there was fairly strong warm advection (red shading) over Minnesota at this time.

The 14Z 850-mb analysis on July 14, 2010. Dark contours denote 850-mb heights. Dashed, red contours are 850-mb isotherms. Wind barbs represent 850-mb winds. Contours filled with blue indicate areas of cold air advection, while red color-filled contours designate areas of warm air advection. Note the rather strong warm advection over Minnesota at this time.

Credit: Storm Prediction Center

This pocket of warm advection was located north of a warm front (12Z surface analysis), and was closely connected to a cluster of thunderstorms that had developed (check out the 14Z regional radar mosaic). Indeed, the severe weather over the Upper Mississippi Valley on July 14, 2010 that you've studied over the past few sections, was not confined to the afternoon hours. Recall that deep, moist convection is possible north of a warm front when there's upper-level divergence above the sloping warm front, where warm-air advection is occurring in concert with overrunning, and that's precisely what happened on the morning of July 14, 2010. Note, however, that the updrafts for such thunderstorms do not originate at the surface. Instead, they originate above the cold stable layer at the surface, and are appropriately called elevated thunderstorms.

Formally, an elevated thunderstorm is a type of deep, moist convection whose updraft originates above the planetary boundary layer. In contrast, updrafts associated with surface-based convection originate at the ground. As a general rule, elevated convection develops above a stable layer of air in the lower troposphere, which means either above a nocturnal inversion, or on the cold side of an anafront (usually warm front or stationary front).

You may have been surprised to see me mention "nocturnal inversions" because you may recall that they typically form on clear nights with calm winds (not exactly the types of nights that make you think "thunderstorms"). But, keep in mind that the entire night need not be clear for nocturnal inversions to form. Indeed, nocturnal inversions can form rather quickly after sunset (a few hours), and the evolving weather pattern could then favor elevated thunderstorms later in the night.

To get a better idea about the contrast between elevated thunderstorms and surface-based thunderstorms, check out the idealized skew-T diagrams below. The sounding on the left is consistent with elevated convection. Note the stable layer (a layer of relatively warm air) between 900 mb and 750 mb (roughly). If unstable parcels of air are lifted from the top of this stable layer, they become positively buoyant, setting the stage for elevated convection (although CAPE is rather small). The sounding on the right favors surface-based convection (surface air parcels lifted to the LFC become dramatically positively buoyant through a deep layer).

(Left) If unstable parcels of air are lifted from the top of the stable layer between 900 mb and 750 mb (approximately), they become positively buoyant, setting the stage for elevated convection (even though CAPE is rather small). (Right) This sounding favors surface-based convection (surface air parcels lifted to the LFC become dramatically positively buoyant through a deep layer). Note that CAPE is noticeably larger.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

So, forecasters look for pockets of warm advection at 850-mb because they can signal overrunning. If lapse rates above the cool, stable layer at the surface are sufficiently steep, elevated thunderstorms can develop, especially if some upper-level divergence is present to give parcels an additional kick of upward motion to get things started.

Low-Level Jet Streams and Moisture Convergence

On the morning of July 14, 2010, we can see the source of the extra kick of upward motion from upper-level divergence on the 12Z NAM model 500-mb analysis of heights and vorticity. Note the weak vorticity maxima present ahead of the closed low centered in south-central Canada.

So, the development of elevated convection in this case was fairly textbook, fitting the conceptual model that you learned about previously. These thunderstorms undoubtedly benefited from the presence of a low-level jet stream over the region, as well. Formally, low-level jet streams are ribbons of relatively fast winds in the lower troposphere driven by strong height gradients.

Why are low-level jet streams of interest? First, they can can efficiently usher moist air into a region (remember that 850 mb is located in the lower troposphere, where most atmospheric water vapor is located). Moist, boundary-layer air rushing into a region can go hand-in-hand with deep moisture convergence. On July 14, 2010, we can see that the low-level jet stream was driven by strong 850-mb height gradients, as shown on the 12Z NAM model analysis of 850-mb heights, temperatures, and winds. From this analysis, should also be able to diagnose the warm advection you saw previously over Minnesota. Note how the 850-mb wind barbs blow across the isotherms (thin, red contours) from higher to lower values.

To better help you focus on the corridor of fast 850-mb winds marking the low-level jet stream, I've annotated its axis on the 14Z analysis of 850-mb wind barbs and isotachs below.

The 14Z analysis of 850-mb winds and 850-mb isotachs (color-filled, in knots) on July 14, 2010. Note the fastest winds over northwest Iowa and Nebraska, where wind speeds exceeded 50 knots. This closed isotach marked the core of a low-level jet stream over the Northern and Central Plains.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0

To get your bearings, wind barbs designate 850-mb winds and color-filled contours indicate 850-mb isotachs (in knots). I've annotated the axis of the low-level jet stream, which passes through the core of its fastest winds, with a white arrow. In this particular case, the core of the low-level jet stream was marked by the area where speeds exceeded 50 knots in western Iowa and eastern Nebraska.

This particular low-level jet stream had its roots over the Gulf of Mexico so there's no doubt that the low-level jet stream was carrying a rich supply of moist air. With such high wind speeds associated with the moist, low-level jet stream, it stands to reason that there would be a spike in moisture convergence in the lower troposhere. We can confirm that with the 14Z analysis of deep moisture convergence from SPC (below), which shows a pocket of deep moisture convergence (red contours) coincident with the ongoing thunderstorms. Revisiting the 14Z 850-mb isotachs above, note that there is some speed convergence associated with the low-level jet stream (fast winds transition to slower winds over Minnesota). Moreover, wind barbs over Minnesota are also confluent, and, in this case, the confluence adds to the overall pattern of convergence.

The 14Z analysis of deep moisture convergence on July 14, 2010. The pocket of deep moisture convergence in northern Minnesota and northwest Wisconsin, marked by solid red contours, corresponded to an ongoing cluster of thunderstorms. The thin green contours indicate the average mixing ratio in the lowest 100 mb of the troposphere.

Credit: Storm Prediction Center

Note that I opted to look at deep moisture convergence instead of surface moisture convergence because SPC's deep moisture convergence product averages the moisture convergence over the lowest two kilometers of the troposphere. Thus, this field often extends high enough to capture the impact of the low-level jet stream (keep in mind that the standard height for 850 mb is 1.5 kilometers). In other words, in cases where there's elevated convection, looking at analyses of surface moist convergence is probably not the way to go, because unstable parcels are feeding into a storm's updraft along a sloping frontal surface, usually a few thousand feet from the earth's surface.

The bottom line is that with moisture convergence occurring near 850 mb, and with upper-level divergence associated with vorticity maxima to the east of the 500-mb closed low that we noted earlier, the stage was set for deep, moist convection (in this case, elevated thunderstorms) over northern Minnesota and northwest Wisconsin on July 14, 2010.

This case gives you a taste of how elevated convection can develop in concert with a low-level jet stream and 850-mb warm advection. But, low-level jet streams can have another important consequence even outside of elevated convection situations. Let's explore.

Low-level Jet Streams and Wind Shear

Speedy winds associated with low-level jet streams can dramatically boost vertical wind shear in the lower troposphere. Because friction slows the wind at the surface of the Earth, fast winds at 850-mb are a good sign that there's a significant change in wind speed with increasing height in the lower troposphere. As we'll explore later, strong vertical wind shear in the lower troposphere, especially in the lowest kilometer, favors tornadogenesis whenever the storm environment supports the initiation of surface-based supercells.

To see an example of a low-level jet stream that caught the eye of forecasters, February 24, 2016 provides a great example. The 20Z Rapid Refresh analysis of 850-mb heights, winds, temperatures, and dew points (below) reveals a robust low-level jet stream along the Eastern Seaboard, to the east of a strong surface low-pressure system centered over the Ohio (check out the 21Z surface analysis). Note the strong height gradient driving wind speeds near 70 knots as far north as Pennsylvania. Clearly, this low-level jet stream was ushering moist air northward, as evidenced by the northward bulge in 850-mb dew points greater than 10 degrees Celsius (shaded in green to indicate moist air).

The 20Z 850-mb analysis on February 24, 2016. Dark contours denote 850-mb heights. Dashed blue and red contours are 850-mb isotherms. Wind barbs represent 850-mb winds. Contours filled with green shading indicate areas with dew points greater than 10 degrees Celsius. Note the potent low-level jet stream along the Eastern Seaboard (winds near 70 knots), and the northward surge of higher dew points that coincided with it.

Credit: Storm Prediction Center

Low-level jet streams of this magnitude (winds near 70 knots) are almost unheard of in the Middle Atlantic States in February. Noting this, forecasters realized that wind shear in the lower troposphere would be quite strong. The 20Z analysis of vertical shear between the surface and an altitude of one kilometer showed that there was a whopping 30 to 60 knots of shear in that layer in the Middle Atlantic States. Recognizing the risk of rotating updrafts in thunderstorms (a component in the development of tornadoes), SPC wisely had issued tornado watches from the Carolinas to Pennsylvania and New Jersey, and indeed, the storm reports for February 24 included 27 tornado reports. Two of those tornadoes occurred in Pennsylvania, which marked only the second and third tornadoes on record in the state during February since 1950.

The bottom line is that you should make an analysis of the 850-mb pattern part of your forecasting routine so that you can keep an eye on temperature advection (particularly warm advection / overrunning), and to detect low-level jet streams (regions of strong height gradients and fast winds). Sometimes these two things go hand-in-hand, but either way the supply of lower tropospheric moisture and the increased low-level vertical wind shear in regions with low-level jet streams are important considerations for forecasters. On February 24, 2016, there's no doubt that the presence of the low-level jet stream helped alert forecasters to an out-of-season tornado risk in the Middle Atlantic States.

So, the 850-mb big-picture pattern should be a crucial part of your forecasting process when trying to predict thunderstorms -- either surface-based or elevated. While areas of 850-mb warm advection / overrunning can help identify hot spots for elevated convection to develop, 850-mb warm advection alone won't make for elevated thunderstorms. In the next section, we're going to look at all of the ingredients needed for elevated convection. Read on.

Read...

In the last section, you learned about the basic difference between elevated and surface-based thunderstorms, namely that an elevated thunderstorm is a type of deep, moist convection with an updraft originating above the planetary boundary layer. In contrast, updrafts associated with surface-based convection originate at the ground. As a reminder, elevated convection develops above a stable layer of air next to the ground (above a nocturnal inversion or above a stable layer on the cool side of anafronts). The environmental temperature profiles that produce elevated thunderstorms also look quite a bit different from those that produce surface-based thunderstorms, as these idealized skew-T diagrams from the last section illustrate.

The most common synoptic-scale set up that results in elevated thunderstorms occurs on the cool side of anafronts, where warm-air advection and upper-level divergence can work in tandem to initiate elevated convection. With these two processes in mind, elevated convection forms where unstable parcels of air feed into the "bottom" of updrafts along the sloping frontal boundary.

While you've seen that general background before, I think the photograph below will really help you conceptualize how elevated convection "works" (a picture is worth a thousand words, right?). The photographer who captured this"striking" photograph had a high vantage point overlooking the Alexander Valley near Santa Rosa, California. At the time, stratus clouds shrouded the valley, indicating a stable layer of air in the lowest levels of the troposphere. Yet, above this stable layer, a bona fide thunderstorm was able to develop--a classic case of elevated convection. If you picture an elevated thunderstorm over stratiform clouds (a stable layer), you'll never confuse elevated convection with surface-based convection.

An elevated thunderstorm over a stable layer in the Alexander Valley near Santa Rosa, California.

Credit: Kent Porter

With your conceptual understanding of elevated convection hopefully cemented, now it's time to dial in on the synoptic patterns and thermal profiles that favor elevated convection. For starters, think back to the cluster of elevated thunderstorms from July 14, 2010 that we discussed previously. Without reservation, the synoptic-scale pattern at the time fit the definition of elevated convection "to a tee" because the thunderstorms formed north of a low-pressure system's warm front (14Z radar reflectivity; 12Z surface analysis). More to the point, warm-air advection and upper-level divergence (associated with vorticity maxima ahead of a closed 500-mb low) paved the way for elevated convection to form along the sloping frontal boundary.

We have yet to examine temperature soundings in the vicinity of these thunderstorms that formed on the morning of July 14, 2010. For sake of argument, let's focus our attention on International Falls, Minnesota, where a thunderstorm occurred at 14Z (check out KINL's meteogram). Below is the 14Z model analysis sounding at International Falls. First, note the deep, saturated layer (relative humidity essentially equal to 100%), which is the skew-T footprint of precipitation. Second, note the strong stability in the layer of air from about 940 mb to roughly 800 mb (this layer of relatively warm air is consistent with warm-air advection north of the warm front). For all practical purposes, unstable parcels of air feeding into the "bottom" of the thunderstorm's updraft originated near 800 mb.

The 14Z (model analysis) temperature and dew-point soundings at International Falls, MN, on July 14, 2010. At the time, unstable parcels of air fed into the bottom of the updraft of an elevated thunderstorm at the top of a stable layer (a layer of relatively warm air) between 940 mb and 800 mb.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0

Any thunderstorm that developed in this environment had to be elevated because a parcel lifted from the surface would never be positively buoyant (it would always remain to the left of the temperature sounding). To drive home this point, please open this interactive tool demonstrating why cool, stable, saturated air near the surface only allows for elevated convection (keep the tool open as you read through the instructions in the following paragraph).

Start by clicking on the red indicator on the right and slowly decrease the pressure level (increase the altitude) of a test air parcel. As you raise the red indicator, you'll see the parcel's moist adiabat (in dark blue). Clearly, the temperature of the air parcel at any point along the moist adiabat is lower than the environment's temperature. In short, the test parcel is negatively buoyant through a deep layer all the way up to pressures approaching 750 mb (the top of the inversion). A test air parcel nudged upward at the top of the temperature inversion would obviously be positively buoyant (note that the local moist adiabat switches from blue to orange at the top of the inversion).

So, the strong temperature inversion starting around 925 mb puts a tight lid on any parcels trying to rise relatively far above the earth's surface. Only air parcels located atop the temperature inversion could rise, in concert with warm-air advection and upper-level divergence to give them an initial boost. So, there's no way convection could be surface-based in this case. Although the inversion is much more dramatic in the interactive tool, the same pattern holds true in the skew-T for International Falls above. Only elevated convection is possible.

Even though CAPE tends to be smaller in elevated convection situations, elevated thunderstorms can still be severe. In most cases, the greatest threat from severe elevated convection is large hail. Damaging winds and tornadoes are still possible with some elevated thunderstorms, but these threats are greatly reduced, depending on the depth of the stable layer of air in the lower troposphere, below the altitude where unstable air parcels feed into the storm's updraft.

Indeed, the speed of downdrafts in elevated storms is often no match for the depth and strength of the stable layer next to the ground. In other words, this stable layer discourages downdrafts from splashing down to earth because air parcels in downdrafts become warmer than their immediate surroundings. Thus, the threat of damaging straight-line winds from elevated storms is rather limited, as is the threat from tornadoes (we'll get into the reasons why stability in the lower troposphere discourages tornadogenesis later). Only when the stable layer is very thin (and stability in the layer is weak) can downdrafts occasionally penetrate to the surface, paving the way for damaging wind gusts, or a rare tornado.

Experienced mesoscale forecasters, like those at SPC, apply this conceptual understanding about the differing severe threats from surface-based and elevated storms regularly in their forecasting routine. For example, on the morning of August 19, 2005, elevated thunderstorms developed across Nebraska, and it's not hard to see why they were elevated based on the skew-T diagram from North Platte, Nebraska, on the right below (note the low-level inversion on the sounding).

(Left) The 12Z composite radar image (large) over the Central Plains on August 19, 2005, shows clusters of thunderstorms over Nebraska. (Right) The 12Z sounding at North Platte, Nebraska, indicates a low-level inversion. For the record, the pressure level at the top of the inversion was roughly 880 mb. Although elevated convection was not occurring at North Platte at this time, this skew-T served as a proxy for the environment in which elevated convection developed.

Credit: WSI / University of Wyoming

On the morning of August 19, a stationary front was draped across Kansas. Nebraska's location on the cool side of an anafront was a "big picture" sign that the convection across the state would be elevated (confirmed by the environment depicted on the skew-T). At 1555Z, forecasters at SPC issued Mesoscale Discussion #2029, which clearly indicated that the initial risk from elevated storms was large hail (and heavy rain). However, as storms developed farther south over Kansas later in the day, forecasters expected storms would become surface-based, increasing the threat of damaging straight-line winds (a couple of tornadoes actually ended up occurring, too).

Elevated convection can be an issue during the cold season, too, and in fact, it helps to explain some of the "weird" winter observations you sometimes hear about or experience: thunder with freezing rain, sleet, or snow. I should note that not all instances of thunder snow, in particular, are a result of elevated convection. Nevertheless, wintry precipitation falls if the environment favors elevated convection and the temperature sounding is entirely below 0 degrees Celsius (a classic snow sounding) or if the lower half of the troposphere makes a warm-air sandwich (a sleet or freezing-rain sounding). Let's explore the topic of wintry precipitation accompanied by thunder by taking a look at a Case Study about one of the worst ice storms ever to occur in Oklahoma.

Read...

In the spirit of 500-mb shortwave troughs, upper-level jet streaks help to prime the local environment for deep, moist convection. If nothing else, upper-level jet streaks promote high-altitude cooling via upward motion associated with pockets of upper-level divergence. Such cooling aloft increases CAPE by moving the environmental temperature sounding to the left on a skew-T. By the way, "upper-level", in the context of jet streaks, typically means 300 mb during the cold season and 250 mb during the warm season. I'll stick with 300 mb here just to make life simpler.

How do we assess upper-level divergence produced by 300-mb jet streaks? Previously, you learned about the good, old four-quadrant model. Remember? This four-quadrant model holds that upper-level divergence occurs in the left-exit and right-entrance regions of 300-mb jet streaks. But, there's a problem with this model--it's highly idealized, and assumes that jet streaks are "straight" (no curvature in the flow).

In the real world, those assumptions aren't realistic. In fact, most upper-level jet streaks are curved. Even the jet streaks that look pretty straight aren't perfectly straight. In contrast to the idealized world of the four-quadrant model, the right-entrance and left-exit regions associated with real-life jet streaks are not sure bets for deep, moist convection.

In real life, the right-entrance and left-exit regions are the most statistically favored quadrants for severe weather, but there are no guarantees. In fact, many an outbreak of severe weather has occurred in the right-exit region of an upper-level jet streak. To understand how this quadrant can be favorable for the development of severe weather, we have to go beyond the simple four-quadrant model of straight jet streaks that you're already familiar with, and think about jet streaks from a different perspective that involves vorticity.

Curvature in the flow within a curved jet streak has some implications for vorticity that changes the patterns of convergence and divergence so that they don't nicely match those from our original four-quadrant model. That's the bottom line, but I'll save the details of the vorticity treatment of jet streaks for the Explore Further section below, if you're interested. Ultimately, however, computer modeling of cyclonically curved jet streaks suggests that a two-quadrant model is more appropriate than any four-quadrant model, as summarized in the schematic below.

The two-quadrant model of a cyclonically curved jet streak (shades of blue indicate wind speeds around its core) . Note that upper-level divergence and the associated upward motion in the left-exit region can "bleed" into the right-exit region.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

Just like straight jet streaks, divergence and upward motion occur in the left-exit regions of cyclonically curved jet streaks. Similarly, convergence and downward motion are hallmarks of the left-entrance regions. But, there are also important differences between the two models. Indeed, upper-level divergence and the associated upward motion “bleed” into the adjacent right-exit region of a cyclonically curved jet streak. Similarly, upper-level convergence and the associated sinking motion can also “bleed” into the right-entrance region.

The bottom line is that with a cyclonically curved jet streak, the right-exit region may be favorable for divergence and upward motion, both of which can help prime the atmosphere for thunderstorm development. So, the right-exit region is not off limits to severe weather. Not by a long shot!

Since no single conceptual model works for all jet streaks, it can be challenging for a forecaster to determine exactly when a jet streak becomes curved enough that the right-exit region becomes favorable for upper-level divergence and upward motion, or exactly where the favorable region of upper-level divergence stops. How does a forecaster deal with these uncertainties?

Personally, I think a somewhat unconventional approach is wise. Let's assume that there's an upper-level jet streak in the vicinity of a region where ingredients in the lower troposphere appear to be coming together for an outbreak of severe thunderstorms. Focusing my attention on the corresponding quadrant of the 300-mb jet streak (above the region of favorable ingredients at low levels), I look for reasons why this specific quadrant might not be favorable for the development of storms. In other words, I automatically assume from the get-go that this quadrant will support deep, moist convection. Then I look for reasons why it might not be favorable. If I can't find any good reasons why it won't be favorable, then I assume that it will help favor deep, moist convection.

That approach might seem odd to you, but as long-time, renowned severe weather forecaster, Jack Hales, likes to say, "People have died in the wrong jet quadrant."  By this he means that low-level uplift and any subsequent eruption of severe thunderstorms are not always constrained to occur in the two most statistically favored quadrants (right-entrance and left-exit regions). To see an example, check out the case from April 26, 1991 in the Case Study box below. It's a prime example supporting Jack's sobering observation, as 72 tornadoes killed 24 people on this date.

Read...

The synoptic-scale set-up for major outbreaks of tornadoes often includes speed maxima in upper-tropospheric and low-level jet streams. In this context, the upper-tropospheric jet stream refers to either the mid-latitude jet stream or the "subtropical jet stream," which is simply a high-altitude band of relatively strong winds located around 30 degrees latitude (which you will study, or may have already studied, in METEO 241).

Lest you get the impression that the intrusion of a newly formed low-level jet stream beneath the left-exit region of an upper-level jet streak is somehow just a huge coincidence, you're about to learn that speed maxima (jet streaks) traveling in the upper-level jet stream can encourage the formation of a low-level jet stream. In such situations, meteorologists say that the upper-tropospheric and low-level jet streams are coupled.

The development of a low-level jet stream in the vicinity of an upper-level jet streak can be a big deal. That's because the presence of a low-level jet stream increases the vertical wind shear in the lowest kilometer of the troposphere. Research has shown that such strong, low-level vertical wind shear heightens the risk of tornadogenesis (assuming the environment is favorable for supercells to erupt), so there's a pretty good big-picture reason for studying the coupling of upper- and low-level jet streams. Let's investigate.

Meteorology of Coupled Jet Streams

The 500-mb height analysis and associated wind barbs at 12Z on November 7, 2004.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0

To understand the concept of coupled upper-level and low-level jet streams, I have to first introduce a new concept: the "ageostrophic wind". As you learned previously, the overall wind flow on the synoptic-scale in the middle and upper troposphere tends to be geostrophic, which means that the pressure-gradient force and Coriolis force are balanced. In this balanced (and idealized) state, the wind blows parallel to local height lines. As you can plainly see on this 500-mb image of the northeastern quarter of the nation at 12Z on November 7, 2004 (on the right), the wind seems to be nearly everywhere parallel to the height contours. I emphasize the word "nearly' because the wind is never perfectly geostrophic. Relatively small imbalances between the pressure-gradient and Coriolis forces result in small accelerations characteristic of most synoptic-scale weather systems.

As original course author, Lee Grenci, likes to say, "You can't fly a kite in the geostrophic wind." The geostrophic wind isn't real--it's idealized. The observed wind always departs from the geostrophic wind, by at least a little bit. This departure from the geostrophic wind is the ageostrophic wind. Thus, we can express the "total wind" (the observed wind) as a vector sum of the geostrophic and ageostrophic components, and believe it or not, you've seen the ageostrophic wind in action before. Jet streaks are a perfect example. The ageostrophic wind is the basis for the divergence / convergence patterns associated with the four-quadrant model of straight jet streaks.

To see what I mean, let's start by assuming that an air parcel is pretty darn close to geostrophic balance as it approaches a jet streak. As it enters the jet streak (remember that air parcels move through jet streaks), the parcel finds itself "subgeostrophic." That's because the parcel's speed, and thus Coriolis force acting on it, no longer match the greater pressure-gradient force (height-gradient force) that is the hallmark of jet streaks. Given this imbalance of forces, the parcel accelerates northward (essentially "downhill") to lower 300-mb heights. At this point, the parcel's velocity has two components, the geostrophic component, which blows from the west, and the ageostrophic component, which blows from the south (see image on the left below). In this region of the jet streak, the northward ageostrophic component of the wind produces the classic mass convergence in the left entrance of a straight jet streak, and divergence in the right entrance.

(Left) For a parcel in the entrance region of a west-to-east, straight jet streak, the ageostrophic wind blows from the south (perpendicular to the major axis of the jet streak). (Right) For a parcel in the exit region of a west-to-east, straight jet streak, the ageostrophic wind blows from the north (perpendicular to the major axis of the jet streak).

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

As the parcel moves toward the core of the jet streak, the ageostrophic wind increases (the parcel continues to accelerate in response to the increasing height gradient). Upon reaching the core of the jet streak, the parcel attains a state of fleeting geostrophy (the parcel's speed and, thus, the Coriolis force acting on it finally are able to offset the height-gradient force). The key word here is "fleeting," because after leaving the core, the parcel quickly finds itself "supergeostrophic." That's because the parcel's breakneck eastward speed now exceeds the geostrophic threshold dictated by the now slightly weaker height-gradient force (the magnitude of the Coriolis force exceeds the magnitude of the height-gradient force). Again, given this imbalance of forces, there must be an acceleration. Indeed, the parcel slows and swerves southward (essentially "uphill") to higher heights. Now the ageostrophic wind blows from the north (see the image on the right above), paving the way for divergence in the left exit and convergence in the right exit.

The key takeaway here is that that the observed wind always has two components: geostrophic and ageostrophic. The geostrophic component is the idealized component (from a "perfect world" that lacks horizontal accelerations), while the ageostrophic component (although sometimes very, very small), accounts for real-life departures from the state of geostrophy. Now with this background out of the way, we can better understand how jet streams can become coupled.

Focus your attention on the idealized schematic below, which shows a 300-mb jet streak (the thin, green lines are 300-mb isotachs). For each wind vector within the jet streak, there is a geostrophic component and an ageostrophic component. The black streamlines pointing southward from the left-exit region indicate the ageostrophic components of the 300-mb winds in the exit region of the jet streak. It's important for you to keep in mind that in reality, the ageostrophic components are small compared to the geostrophic components. On a 300-mb chart, you would only observe westerly winds (not northerly winds) in this scenario, but on very close inspection, these westerly winds would have a slight southward deviation. This slight southward swerve would be the footprint of the ageostrophic wind. The bottom line here is that you would never observe streamlines like the black ones below, on a standard 300-mb analysis. For sake of this presentation, we artificially removed the geostrophic components so you can better see the otherwise very subtle contributions of the ageostrophic wind.

An idealized schematic showing the transverse circulation (black arrows) in the exit region of a 300-mb jet streak. In response to low-level pressure falls beneath the area of upper-level divergence in the left-exit region, a southerly ageostrophic component develops. In turn, the associated horizontal acceleration can help to generate a low-level jet stream (thick orange arrow). In this context, the upper-level and low-level jet streams are coupled.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

Any way you slice it, the ageostrophic flow of air in the exit region produces upper-level divergence in the left-exit region. In response, a region of negative pressure tendencies develops in the lower troposphere beneath the area of upper-level divergence. In turn, this pocket of pressure falls causes low-level southerly winds to accelerate, which often paves the way for a low-level jet stream.

With the idea of coupled jet streams in mind, a low-level, southeasterly jet stream can develop over California during winter in concert with an arriving 300-mb jet streak. Such a low-level jet stream rapidly transports moisture northward and increases the low-level vertical wind shear (and thus heightens the risk of California tornadoes). Yes, tornadoes form in California, mostly in the wintertime. Let's investigate.

Severe Weather in California

The Storm Prediction Center occasionally issues severe-thunderstorm and tornado watches during the cold season for California's Central Valley when conditions are favorable for supercells to form. As a general rule, California supercells erupt behind cold fronts associated with strong, occluded mid-latitude cyclones. In such situations, mid-level lapse rates steepen as the trailing, cold 500-mb low starts to move inland. Vertical wind shear in the lowest six kilometers increases, and a strong 300-mb jet streak typically induces a low-level jet stream. The schematic below shows the classic synoptic set-up for severe thunderstorms in the Central Valley during the cold season.

The synoptic set-up for an outbreak of severe thunderstorms in California during the cold season. A 300-mb jet streak approaching California is coupled with a low-level jet stream over the Central Valley.

Credit: David Babb © Penn State is licensed under CC BY-NC-SA 4.0

Let's examine this pattern favorable for severe weather more closely. When a strong low-pressure system approaches the California Coast during winter, the cold front can sweep inland relatively far east of the longitude of the surface low. The west-southwesterly flow behind the advancing cold front then paves the way for a lee trough to form in California's Central Valley. Meanwhile, with the surface low still lingering offshore (northwest of San Francisco, for example), California's Central Valley channels the low-level flow of air, causing the expected southwesterly, post-frontal winds to blow from the southeast instead. These south-easterlies can become a bona fide low-level jet stream in response to upper-level divergence in the left-exit region of a 300-mb jet streak. Meanwhile, the trailing 500-mb trough often deepens (intensifies), producing robust southwesterly or westerly winds in the middle troposphere (which, of course, enhances vertical wind shear in the first six kilometers of the troposphere).

Such patterns are conducive to small supercells erupting in the Central Valley. The bottom line here is that most of California's infrequent but recognizable regional severe weather events typically occur in concert with low-level southeasterly (and post frontal) winds during the cold season. But, there's a slightly different "twist" to this general pattern whenever cold-season tornadoes develop in the the Los Angeles metropolitan area. Tornadoes in Los Angeles? No, this isn't the set up for a horribly cheesy sci-fi movie. On occasion, tornadoes really do happen near Los Angeles! To see what I mean, check out the Case Study below.