Lesson 5: Escalated, Nominal Price and Real Price

Lesson 5: Escalated, Nominal Price and Real Price sxr133

Introduction

Introduction msm26

Overview

This lesson addresses the issues of constant, escalated values, nominal, and real prices, which are very important for project evaluation reaching several years into the future. In this lesson, you will learn the factors that will be considered in escalation and inflation as well as different factors to be considered in constant dollar and escalated dollar. Two examples will be shown on escalated and constant dollar ROR analysis and NPV analysis. An equation is also important and commonly used to convert escalated dollar ROR to constant dollar ROR with assumption of the inflation rate.

Learning Objectives

At the successful completion of this lesson, students should be able to:

  • differentiate among the factors to be considered in escalation and inflation;
  • differentiate among the factors to be considered in constant dollar and escalated dollar;
  • understand how to conduct ROR and NPV analysis with escalated and constant dollar; and
  • be fluent with the equation to convert between escalated dollar ROR and constant dollar ROR.

What is due for Lesson 5?

This lesson will take us one week to complete. Please refer to the Course Syllabus for specific time frames and due dates. Specific directions for the assignment listed below can be found within this lesson.

Lesson 5: Reading and Assignment
ReadingRead Chapter 5 of the textbook and lesson 5 in this website.
AssignmentHomework and Quiz 5.

Questions?

If you have any questions, please post them to our discussion forum, located under the Modules tab in Canvas. I will check that discussion forum daily to respond. While you are there, feel free to post your own responses if you, too, are able to help out a classmate.

Inflation and Escalation in Economics

Inflation and Escalation in Economics ksc17

Inflation

Inflation is an economic term that indicates the increase in price of goods and services over time and can be more precisely defined as “a persistent rise in the prices associated with a basket of goods and services that is not offset by increased productivity.” Inflation causes purchasing power to reduce (more information can be found at Inflation (Investopedia) and at Inflation (Wikipedia). Inflation affects almost everything in the financial market and it is measured and reported by various indexes. The most common index for determining the inflation rate is called the Consumer Price Index or CPI. You can read more about the CPI at the Wikipedia page for Consumer Price Index. Monthly CPI reports are published at the U.S. Bureau of Labor Statistics website.

Escalation

"Escalation refers to a persistent rise in the price of specific commodities, goods, or services due to a combination of inflation, supply/demand, and other effects such as environmental and engineering changes." Factors that affect the escalation include:

  • Inflation
  • Supply/demand
  • Technological Changes
  • Environmental Effects
  • Political Effects
  • Miscellaneous Effects

As defined above, inflation refers to the increased price of a basket of goods and services, while escalation refers to an increase in price of a specified good or service. Inflation is one of the factors that cause escalation. The Alaskan pipeline is a good example that can help with understanding the difference between inflation and escalation. This pipeline was estimated to cost about 900 million dollars in 1969, while the final estimate in 1977 came to about 8 billion dollars for the project, which is around 900% higher than the initial estimation. You should note that just a portion of this increase was due to the inflation rate and that other factors such as supply/demand effects on labor and materials, and environmental and technology changes also contributed to the substantial increase in costs.

There are two techniques used to take into account the effect of inflation and escalation in economic analysis. Both methods should lead into the same results:

1. Escalated dollar analysis

"Escalated dollar values refer to actual dollars of revenue or cost that will be realized or incurred at a specific future point in time."

2. Constant dollar analysis

"Constant dollar values refer to hypothetical constant purchasing power dollars obtained by discounting escalated dollar values at the inflation rate to some arbitrary point in time, which often is the time that corresponds to the beginning of a project. Constant dollars are referred to as real dollars or deflated dollars in many places in the literature."

Escalated dollar analysis considers different purchasing power for different points in time, while constant dollar analysis aims to set a same base and a constant purchasing power for all points in time. Constant dollar analysis requires more calculation and the chance of making mistakes increases, while escalated dollar analysis has more reliable results. Escalated dollar and constant dollar analysis are two different methods and their results shouldn’t be compared. A common mistake in applying the results of constant dollar analysis is to compare the calculated constant dollar ROR with other escalated dollars investment opportunities such as bank interest rate and so on. Therefore, constant dollar ROR for alternative investment opportunities (constant dollar minimum rate of return) should be the base for comparing and evaluating constant dollar analysis for an investment project.

Usually reported cost, revenue, and incomes occurring in different points of time are reported at today’s dollar. Escalated dollar approach applies an assumed escalation rate to predict and increase the sums over time. To do so, similar to compounding technique, a single payment compound amount factor (F/Pi,n) has to be multiplied by the amount, and escalation rate has to be substituted for i.

For example, consider an investment with the following cashflow:

C0=$10,000C1=$10,000I2=$15,000I3=$15,000
0123

C: Capital Cost, I: Income

Assuming an escalation rate of 12%, escalated dollar cashflow is:

C0=$10,000C1=$10,000*(F/P12%,1)
=$11,200		I2=$15,000*(F/P12%,2)
=$18,816		I3=$15,000*(F/P12%,3)
=$21,074
0123

Please watch the following video (6:25) Inflation, escalation, and escalated dollar analysis.

Inflation, escalation, and escalated dollar analysis

PRESENTER: In this video, I will explain how to consider inflation and escalation in the economic evaluation of investing project. Inflation is the economic term that indicates the average increase in price over the time. It is usually calculated for a basket of goods or services.

The most common index for determining the inflation rate is called CPI, or Consumer Price Index, and it is published by US Bureau of Labor Statistics. For example, the percentage change in CPI in a year compared to previous year indicates the inflation rate for that year.

Inflation causes purchasing power to reduce. For example, if you had $100 last year and the inflation rate is 5%, it means you won't be able to buy the same thing that you could buy last year. You can buy less.

Escalation is also referred to the price increase, but it is defined for only one good or service. Inflation is reported for basket of goods or service, and it is kind of a general average for the entire economy. But escalation is only for one good or service. So if price of a good or service increases, it can be because of inflation, supply and demand change, technological change, environmental effects, or political effects.

Two techniques are used to take into account the effect of inflation and escalation in economic analysis. Both of them should give you the same result. These two are called escalated dollar and constant dollar.

In escalated dollar analysis, you let your values, payments, income, costs, to be increased according to an escalation rate. In the constant dollar analysis, you will remove the effect of inflation from the increase value, from the escalated cash flow, meaning that you want to consider a hypothetical constant purchasing power.

One thing that you should keep in mind is you can do the constant dollar analysis only when you consider the escalation, only after escalated dollar analysis is done. Escalated and constant dollar analysis are two different methods, and the result shouldn't be compared.

Usually the reported cost, revenue and incomes are happening at different time, and they're reported at today's dollar. Escalated dollar analysis lets you apply the escalation rates to these payments. You assume an escalation rate, and you will predict the increase of each payment over the time.

In order to calculate the escalated dollar cash flow, you will compound each year's payment by the escalation rate, and you will have the escalation cash flow. If you do that for every single year for all the payments, you will have escalated cash flow in the end.

So let's work on this example. Assume this cash flow. We are going to have the investments of $10,000 at the present time and in year 1, and we are going to have the income of $15,000 at year 2 and year 3.

So let's calculate the escalated cash flow, the escalated dollar cash flow, for this investment, considering the escalation rate of 12%. As I explained in previous slides, in order to calculate the escalated dollar cash flow, we need to compound each payment by the escalation rate of 12%. So we need to multiply each year's cash flow by the factor F over P and the escalation rate.

So as you can see here, the present time payment is not going to be affected by the escalation. The first payment, which was at year 1, is going to be multiplied by the factor F over P, 12% of escalation rate, and 1 year of compounding. And the same for the other payments. So the $15,000 of income in the year 2 is going to be compounded for 2 years and 12% of escalation rate, and last year, year 3, it has to be compounded for 3 years by 12% of escalation rate.

And we calculate the result for each year. So the result is going to show us the escalated dollar cash flow considering the escalation rate of 12% for the original cash flow.

In order to calculate escalated dollar cash flow, we need to consider an escalation rate. Many, many investors use the anticipated inflation rate as the escalation rate to calculate the escalated dollar cash flow. But there are commodities, such as construction equipment, steel, concrete, labor, and energy, that may not follow this approximation. We can also have the negative escalation rate in case we are going to anticipate any decrease in costs, revenue, or income.

Credit: Farid Tayari

Escalation rate includes the inflation rate, and constant dollar approach applies a constant purchasing power by removing the effect of inflation rate from escalated dollars. Inflation effect can be removed, similar to discounting technique, by multiplying the single payment present worth factor (P/Fi,n) by escalated dollars and applying inflation rate as i. Many investors choose to utilize the anticipated inflation over future years as an approximation for escalation. Commodity prices, the price for construction equipment, steel, concrete, labor, and energy, may not move in direct correlation with the rate of inflation. Note that negative escalation rate can also be applied, if decrease in costs, revenue, or income is anticipated.

For example, considering inflation rate of 6% for above escalated dollar cashflow, constant dollar cashflow can be calculated as:

C0=$10,000C1=$11,200*(P/F6%,1)
=$10,566.04		I2=$18,816*(P/F6%,2)
=$16,746.17		I3=$21,074*(P/F6%,3)
=$17,694.07
0123

Please watch the following video (4:11): Constant dollar analysis.

Constant dollar analysis

PRESENTER: In this video, I'm going to explain how to apply the constant dollar analysis on an escalated cash flow for a project evaluation. As I explained in previous video, inflation is an indication that shows the increase in the price of a basket of goods or services over the time. But escalation is an indication of a price increase for one good or service.

I explain that we can calculate the escalated cash flow, escalated dollar cash flow, by the compounding payment at each year by the escalation rate. In the constant dollar technique, we will try to remove the effect of inflation in considering constant purchasing power. Because the escalation rate includes inflation, and we want to remove this effect and consider the hypothetical constant purchasing power. We can remove the effect of inflation from the escalated dollar cash flow by discounting payment at each year, considering that the inflation rate.

Let me explain how to calculate the constant dollar cash flow in an example. So in previous example in a previous video, we apply the escalation rate of 12% for the given cash flow that we had. So in order to calculate the escalated dollar cash flow, we compound each year's payment, each payment, by 12% escalation rate, and we calculated the escalated dollar cash flow, which is the escalated dollar cash flow, as you can see here.

So now we want to remove the effect of inflation rates and calculate the constant dollar cash flow. Please note that constant dollar cash flow can be calculated only after you already calculated the escalated dollar cash flow. You already consider it an escalation for your payments. Now, you want to remove the effect of inflation, and you want to consider the constant purchasing power and calculate, which means calculating constant dollar cash flow.

So in order to calculate the constant dollar cash flow, we need to discount each year payment, each year cash flow, by the inflation rate. So present time payment is not going to be affected by any inflation or escalation. Escalated payments at year one, $11,200. So we want to calculate the constant dollar for this payment. We multiply it by-- we discount it by one year, and 6%, and so on for the other payments.

Year three, we discounted for three discounting period and 6% of inflation rate. And the result. So the escalated dollar of $11,200 in the year 1 equals the constant dollar of $10,566. It means considering the inflation rate, the escalated dollar of $11,200 in the year one has the same purchasing power as $10,566 at the present time.

Credit: Farid Tayari

Last but not least, gold has been considered a good hedge against the long-term impact of inflation. Back in 1990, the gold price was $420 per ounce. In 2000, price fell to about $275 per ounce. That means an annual price decline of 4.1% per year over 10 years. During the same period, US inflation (as measured by CPI) averaged approximately 3% per year. If gold price would have increased in value at the rate of inflation, the value in 2000 would have been:

420*( F/ P 3%,10 )=420*1.3439=$564/ounce

Instead, the actual price dropped to $275 per ounce and the corresponding constant dollar equivalent price of gold dropped to

275*( P/ F 3%,10 )=275*0.7441=$205/ounce

In 2008, the gold trading price was $925 per ounce, an investment in an ounce of gold in 1990 would have produced an average annual rate of return of

0=−420+925*( P/ F i,18 ) i=ROR=4.48%

After adjusting for an assumed 3% per year inflation, the real return on your investment would be closer to 1.4% per year. The calculations related to this type of constant dollar measure of economic performance will be developed in the Example 5-1 on the next page.

Practice Example:

Currently (May 2020) gold is trading at around $1,700 per ounce. How much would be the average annual rate of return of an investment in one ounce of gold in 1990? How much would be the rate of return, adjusted for inflation, assuming 3% per year of inflation in average?

Answer: 4.77% and 1.7% (approx.)

Italicized sections are from Stermole, F.J., Stermole, J.M. (2014) Economic Evaluation and Investment Decision Methods, 14th edition. Lakewood, Colorado: Investment Evaluations Co.

Escalated and Constant Dollar Cash Flow

Escalated and Constant Dollar Cash Flow jls164

The following examples can help you better understand escalated and constant dollar analysis.

Example 5-1:

Calculate the ROR for the investment that includes 1,000 and 1,200 dollar costs at the present time and at the end of the first year, which yields 800, 1,200, and 1,600 dollars of income at the end of the second, third, and fourth years. There is no salvage value.

Cash flow for this investment can be shown as:

C0=$1,000C1=$1,200I2=$800I3=$1,200I4=$1,600
01234
Present value of all costs=present value of all incomes present value of all costs= C 0 + C 1 *( P/Fi,1 )=1,000+1,200*[ 1/( 1+i )1 ] present value of all incomes= I 2 *( P/ F i,2 )+ I 3 *( P/Fi,3 )+I4*( P/Fi,4 ) =800*[ 1/( 1+i )>2 ]+1,200*[ 1/( 1+i ) ]+1,600*[ 1/( 1+i )4 ] 1,000+1,200*[ 1/( 1+i )1 ]=800*[ 1/( 1+i )2 ]+1,200*[ 1/( 1+i )3 ]+1,600*[ 1/( 1+i )4 ] or 0=−1,000−1,200*[ 1/( 1+i )1 ]+[ 800*1/( 1+i )2 ]+1,200*[ 1/( 1+i )3 ]+1,600*[ 1/( 1+i )4 ]

By the trial and error method or with the IRR formula in Microsoft Excel, ROR for this project is calculated as: i=20.5%.

Figure 5-1 shows how this problem can be formulated in Microsoft Excel.

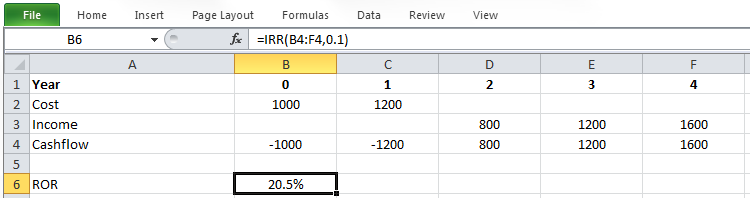
Excel screen capture of calculating ROR. Described in surrounding text
Figure 5-1: Calculating ROR using IRR function in Microsoft Excel.
Credit: Farid Tayari

Escalated Dollar Analysis

Example 5-2:

Now assume for the above investment, costs and incomes will be escalated with the rate of 18% and 12% per year. Calculate the escalated dollar ROR for this investment.

For the escalated method, we need to utilize single payment compound amount factors (F/Pi,n) to convert (compound) the today’s dollar value to escalated dollar regarding the escalation rate:

C0=$1,000C1=$1,200*(F/P18%,1)
=1,416		I2=$800*(F/P12%,2)
=1,003.52		I3=$1,200*(F/P12%,3)
=1,685.91		I4=$1,600*(F/P12%,4)
=2,517.63
01234

Note that escalation has no effect on the cost in the present time (1,000 dollars) because it assumes that all the amounts happen at the end of the year.

The rest of the solution for determining ROR is similar to before:

Present value of all costs=present value of all incomes present value of all costs= C 0 + C 1 *( P/Fi,1 )=1,000+1,416*[ 1/( 1+i )1 ] present value of all incomes= I 2 *( P/ F i,2 )+ I 3 *( P/Fi,3 )+I4*( P/Fi,4 ) =1,003.52*[ 1/( 1+i )2 ]+1,685.91*[ 1/( 1+i )3 ]+2,517.63*[ 1/( 1+i )4 ] 1,000+1,416*[ 1/( 1+i )1 ]=1,003.52*[ 1/( 1+i )2 ]+1,685.91*[ 1/( 1+i )3 ] +2,517.63*[ 1/( 1+i )4 ] or 0 =−1,000−1,416*[ 1/( 1+i )1 ]+1,003.52*[ 1/( 1+i )2 ]+1,685.91*[ 1/( 1+i )3 ] +2,517.63*[ 1/( 1+i )4 ]

And ROR for this project is calculated as: i=33.6%. Figure 5-2 displays the way this problem can be formulated in Microsoft Excel..

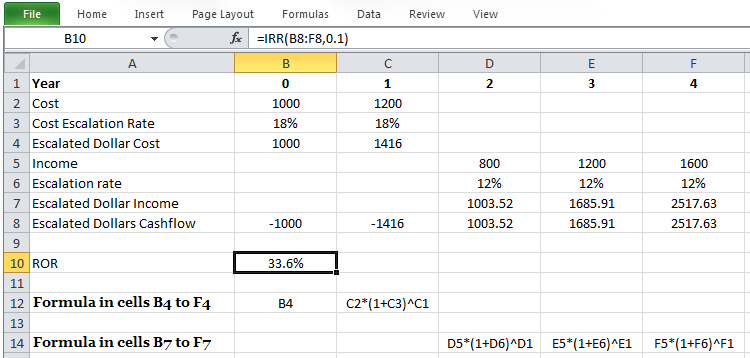
Excel screen capture of calculating ROR. Described in surrounding text
Figure 5-2: Calculating ROR applying Escalated Dollar Analysis in Microsoft Excel.
Credit: Farid Tayari

Constant Dollar Analysis

Example 5-3:

Now, determine the constant dollar ROR for the investment explained in Example 5-2 assuming an annual inflation rate of 15%.

In order to remove the effect of the inflation rate from our calculations, we need to discount the escalated dollars from previous analysis at the rate of inflation to express all dollar values in terms of time zero purchasing power. It can be done using the single payment present worth factor (P/Fi,n) with the assumed inflation rate.

C0=$1,000C1=$1,416*(P/F15%,1)
=1,231.30		I2=$1,003.52*(P/F15%,2)
= 758.81		I3=$1,685.91*(P/F15%,3)
= 1,108.52		I4=$2,517.63*(P/F15%,4)
= 1,439.46
01234

Here, $1,231.30 at year 0 would purchase the goods and service that $1,416 would purchase at year 1, if inflation is 15% per year. $758.81 at year 0 would purchase the goods and services that $1,003.52 would purchase at year 2 if inflation is 15% per year and so on. The rest of the calculations are similar to before:

Present value of all costs=present value of all incomes present value of all costs= C 0 + C 1 *( P/Fi',1 )=1,000+1,231.3*[ 1/( 1+i' )1 ] present value of all incomes=758.81*[ 1/( 1+i' )2 ]+1,108.52*[ 1/( 1+i' )3 ] +1,439.46*[ 1/( 1+i' )4 ] 1,000+1,231.3*[ 1/( 1+i' )1 ]=758.81*[ 1/( 1+i' )2 ]+1,108.52*[ 1/( 1+i' )3 ] +1,439.46*[ 1/( 1+i' )4 ]

Where i' equals constant dollar ROR. And i'= 16.2% is calculated as ROR for constant dollar.

The following figure displays how constant dollar analysis can be formulated in Microsoft Excel.

Excel screen capture of calculating ROR. Described in surrounding text
Figure 5-3: Calculating ROR applying Constant Dollar Analysis in Microsoft Excel.
Credit: Farid Tayari

Please watch the following video (6:28): Escalated and constant dollar rate of return analysis.

Escalated and constant dollar rate of return analysis

PRESENTER: Let's work on an example to calculate the rate of return for escalated dollar cash flow and also constant dollar cash flow. This cash flow is given for an investment. So let's calculate the rate of return. In order to calculate the rate of return, we'd write the equation,the present value of costs equals the present value of income plus the present value of salvage. We don't have salvage value here. So the present value of costs equals the present value of income. We have two costs here-- $1,000 at present time and $1,200 at year one. And we're going to have three incomes of $800, $1,200, and $1,600 in a year two, three, and four.

So we write the equation and solve it for I and calculate the rate of return as 20.5%. Now let's consider an escalation rate of 18% for costs and escalation rate of 12% for income. Let's calculate the escalated dollar cash flow and then we will calculate the rate of return for the escalated dollar cash flow. In order to calculate the escalated dollar cash flow, we need to compound each payment by the escalation rate and considering the compound periods.

The payment at year 0 is not going to be affected by the escalation. So it stays unchanged. The cost of $1,200 at year 1 will be compounded with an 18% escalation rate because this is a cost and the compounding period will be 1. The income of $800 at year 2 will be escalated with 12% because this is an income and the compounding period will be two years and so on-- the income of $1,200 at year three, 12% escalation rate and three years compounding period and $1,600 income, 12% escalation rate and 4 compounding period-- and the result.

So we are going to have escalated cash flow at this cash flow that we can see here. And we want to calculate the rate of return for this escalated dollar cash flow. Again, we write the equation, the present value of cost equals the present value of all income. We have 2 costs here-- $1,000 and $1,416, which are escalating dollar cash flow. So if we write the equation, the present value of costs equals the present value of income, we have three incomes here-- the income at year 2, income at year 3, and income at year 4.

And we solve this equation for I. And we calculate that escalated dollar rate of return as 33.6%. So we calculated our escalated cash flow as the cash that you can see here. Now let's consider the inflation rate of 15%, and let's calculate the constant dollar cash flow and then calculate the rate of return for the constant dollar cash flow.

In order to remove the effect of the inflation rate from our calculations, from our escalated dollar cash flow, we need to discount each payment in the escalated cash flow by the inflation rate and considering the discounting period. So we need to multiply each payment and the escalated cash flow by the single payment present worth factor or factor p over f, considering the inflation rate and the discounting period to calculate the constant dollar cash flow. So as you can see here, we discount each payment by the inflation rate, which was 15%, and the discounting period.

You know that the present time is not going to be affected by the inflation rate. So we start from year 1, the escalated dollar cash flow. We multiply it by the single payment prison worth factor. This 15% is the inflation rate. And 1 is the discounting period. For year 2, the same inflation rates. The discounted period is going to be 2, and so on for year 3 and year 4.

And we calculate the result, which shows the constant dollar cash flow. So it means, for example, $1,231 at year 0 would have the same purchasing power as $1,416 in year 1. And let's calculate the rate of return for these constant dollar cash flow. Again, the equation is the present value of cost equals the present value of income. We have two constant-dollar costs and three incomes. So if we write the equation and we solve it for I and we calculate that the constant dollar rate of return as 16.2%. So we show it with I prime. And it is the constant dollar rate of return.

Credit: Farid Tayari

After calculating the ROR for the project, in order to complete the assessment and make the proper decision, it is necessary to compare it with the minimum rate of return (that is determined by other investment opportunities) to see if the project is economically satisfactory. To do so, you should be very careful using the proper minimum rate of return that is reported in escalated or constant dollars. For example, if other investment opportunities give 25% ROR on escalated dollars (it means the minimum rate of return on escalated dollars is 25%), we can conclude that this project with ROR of 33.6% is economically satisfactory. But the minimum rate of return of 25% on escalated dollars can’t be compared with the calculated 16.2% constant dollar.

As you can see in Example 5-2 and 5-3 for ROR calculations, P/Fi,n and P/Ff,n * P/Fi’,nsub> are similar:

P/ F i,n =P/ F f,n *P/ F i’,n 1/ ( 1+i ) n =1/ ( 1+f ) n *1/ ( 1+i’ ) n ( 1+i )=( 1+f )*( 1+i’ ) i'=[ ( 1+i )/( 1+f ) ]−1
i'=[ ( 1+i )/( 1+f ) ]−1
Equation 5-1
 

i: escalated dollar ROR
i': constant dollar ROR
f: inflation rate

This mathematical proof is known as the “Fisher Rule.” This equation is a simpler way for calculating constant dollar ROR given the inflation rate and escalated dollar ROR. For example, i= 33.6% was calculated in Example 5-2 as ROR for escalated dollar analysis. In Example 5-3, ROR for a constant dollar is asked for the inflation rate of 15%. According to Equation 5-1, equals constant dollar ROR can be determined:

i'=[ ( 1+i )/( 1+f ) ]−1 i'=[ ( 1+0.336 )/( 1+0.15 ) ]−1=1.162−1=0.162=16.2%

Which is equal to the Example 5-3 results.

Equation 5-1 can also be utilized to determine the minimum rate of return for constant dollars knowing the inflation rate and minimum rate of return for escalated dollars. In this case, i should be replaced with i* and i' with i'*:

i'*=[ ( 1+i* )/( 1+f ) ]−1
Equation 5-2
 

i*: escalated dollar minimum rate of return
i'*: constant dollar minimum rate of return
f: inflation rate

For example, if the minimum rate of return (for other investment opportunities) for escalated dollars is considered 25%, the minimum rate of return for constant dollar assuming an inflation rate of 15% can be calculated as:

i'*=[ ( 1+i* )/( 1+f ) ]−1 i'=[ ( 1+0.25 )/( 1+0.15 ) ]−1=1.087−1 =0.087=8.7%

Please watch the following video (6:41): The Fisher Rule.

Fisher Rule

PRESENTER: In this video, I'm going to explain how to use the Fisher Rule to convert the escalated dollar and constant dollar rates. So, in the previous example, we calculated the rate of return for the escalated dollar cash flow and also for the constant dollar cash flow. But after we calculate the rate of return, we need to compare it with something with a minimum rate of return to conclude that if we're going to have a good investment or not, if the project is going to be economically satisfactory or this is not going to be a good project.

Here is a summary of the previous example's results. So this is the escalated dollar cash flow. And the rate of return for escalated dollar cash flow is 33.6%. And this is the constant dollar cash flow that we calculated. And the rate of return for constant dollar cash flow was 16.2.

So we have two rates of returns, the escalated dollar cash flow rate of return and constant dollar cash flow rate of return. So, for example, if we have other investment opportunities that give a 25% rate of return on the escalated dollar cash flow, then we can conclude that this is a good investment because the escalated dollar cash flow is 33.6% and we can conclude that this project is economically satisfactory. But the minimum rate of return of 25% on the escalated dollar cannot be applied to the constant dollar rate of return. This is a very important point that you should always be very careful about.

So as you saw in previous slides, escalated dollar rates cannot be compared with the constant dollar rates. So the Fisher Rule is the equation that helps us compare and convert these rates. I wrote the equation here. I is the escalated dollar rate of return. I prime is the constant dollar rate of return and f is the inflation rate.

So you can calculate any of these from the other two. And this is applicable for any other rates. So here its for the rate of return. But you can use this equation for any other rates that you need to convert for the escalated dollar or the constant dollar.

So using this equation, we can simply calculate the constant dollar rate of return given the inflation rate and escalated dollar rate of return. So we can calculate any rate, any constant dollar rate, given the inflation rates and constant dollar rate.

So, for example, we calculated the escalated dollar rate of return as 33.6% and we considered the 15% of inflation rate. Knowing these two, using the Fisher Rule, we can easily calculate the constant dollar rate of return. So we just plug the i and f escalated dollar rates and inflation rate and we calculate the i prime or the rates, the constant dollar rate, as 16.2, which is exactly the same as what we calculated for the constant dollar rate of return.

So again, Fisher Rule can be used to convert any escalated dollar rate to the constant dollar rate using the inflation rate. For example, using the Fisher Rule, we can calculate the minimum rate of return for the constant dollar given the inflation rate and the minimum rate of return for the escalated dollars. So we'll rewrite the equation as the equation 5-2. I star is an escalated dollar minimum rate of return. I prime star is the constant dollar minimum rate of return. And f is the inflation rate.

So going back to the previous example, the escalated dollar minimum rate of return was considered as 25%. So if we want to calculate the minimum rate of return for constant dollar, we can use the Fisher Rule and consider the inflation rate of 15% and calculate the minimum rate of return for the constant dollar as 8.6%. Please remember we calculated the escalated dollar cash flow as 33.6%. And the minimum rate of return for the escalated dollar cash flow is 25%. And then we concluded that, because the rate of return is higher than the minimum rate of return, this project is economically satisfactory.

But we said that you cannot compare the constant dollar cash flow rate of return with this 25%. So we need to calculate. We needed to calculate the minimum rate of return for constant dollar cash flow. And that's what we calculated as 8.7%.

So because the 16.2% rate of return for the constant dollar cash flow is higher than 8.7% of the minimum rate of return for the constant dollar cash flow, we can conclude that this project is economically satisfactory. So our new base to compare the constant dollar cash flow is the constant dollar minimum rate of return of 8.6%

Credit: Farid Tayari

Escalated and Constant Dollar ROR and NPV

Escalated and Constant Dollar ROR and NPV jls164

This section provides more examples of how to evaluate the economic potential of an investment project based on ROR and NPV analysis. In the following example, the escalated dollar minimum ROR is assumed 15%, and the inflation rate will be 6%. As previously explained, Equation 5-2 can be applied to calculate the constant dollar minimum rate of return.

Example 5-4:

Calculate ROR for the investment that has the following projected today’s dollar costs and revenue:

C0=$50,000C1=$80,000Rev2=$100,000
OC2=30,000		Rev3=$90,000
OC3=30,000		Rev4=$80,000
OC4=30,000		L=0
01234

C: Capital Cost, OC: Operating Cost, Rev: Revenue, L: Salvage

Present value of all costs = present value of all revenue

Present value of all costs= C 0 + C 1 *( P/ F i,1 )+O C 2 *( P/ F i,2 )+O C 3 *( P/ F i,3 )+OC4*( P/ F i,4 ) =50,000+80,000*[ 1/ ( 1+i ) 1 ]+30,000*[ 1/ ( 1+i ) 2 ]+30,000*[ 1/ ( 1+i ) 3 ]+30,000*[ 1/ ( 1+i ) 4 ]
Present value of all revenues=Re v 2 *( P/ F i,2 )+Re v 3 *( P/ F i,2 )+Re v 4 *( P/ F i,4 ) =100,000*[ 1/ ( 1+i ) 2 ]+90,000*[ 1/ ( 1+i ) 3 ]+80,000*[ 1/ ( 1+i ) 4 ]

50,000+80,000*[ 1/ ( 1+i ) 1 ]+30,000*[ 1/ ( 1+i ) 2 ]+30,000*[ 1/ ( 1+i ) 3 ]+30,000*[ 1/ ( 1+i ) 4 ] =100,000*[ 1/ ( 1+i ) 2 ]+90,000*[ 1/ ( 1+i ) 3 ]+80,000*[ 1/ ( 1+i ) 4 ]0 =−50,000−80,000*[ 1/ ( 1+i ) 1 ]+70,000*[ 1/ ( 1+i ) 2 ]+60,000*[ 1/ ( 1+i ) 3 ]+50,000*[ 1/ ( 1+i ) 4 ]

So, ROR can be calculated as i = 15.61%.

Excel screen capture of Calculating ROR
Figure 5-4: Calculating ROR in Microsoft Excel.
Credit: Farid Tayari

Example 5-5:

Now, assume escalation rates of 8% per year for capital cost (development cost), 12% per year for operating costs and 10% per year for revenues. Calculate ROR and NPV for this investment, and make escalated dollar analysis considering 15% escalated dollar minimum rate of return, i*.

C0=$50,000C1=$80,000*(F/P8%,1)
=86,400		Rev2=$100,000*(F/P10%,2)
=121,000
OC2=30,000*(F/P12%,2)
=37,632		Rev3=$90,000*(F/P10%,3)
=119,790
OC3=30,000*(F/P12%,3)
=42,148		Rev4=$80,000*(F/P10%,4)
=117,128
OC4=30,000*(F/P12%,4)
=47,206
01234

Present value of all costs = present value of all revenues

Present value of all costs= C 0 + C 1 *( P/F i,1 )+O C 2 *( P/F i,2 )+O C 3 *( P/F i,3 )+O C 4 *( P/F i,4 ) =50,000+86,400*[ 1/( 1+ i )1 ]+37,632*[ 1/( 1+ i )2 ]+41,148*[ 1/( 1+ i )3 ]+47,206*[ 1/( 1+ i )4 ]
Present value of all revenues=Re v 2 *( P/ F i,2 )+Re v 3 *( P/ F i,2 )+Re v 4 *( P/F i,4 ) =121,000*[ 1/( 1+ i )2 ]+119,790*[ 1/( 1+ i )3 ]+117,128*[ 1/( 1+ i )4 ]
50,000+86,400*[ 1/( 1+ i )1 ]+37,632*[ 1/( 1+ i )2 ]+41,148*[ 1/( 1+ i )3 ]+47,206*[ 1/( 1+ i )4 ] =121,000*[ 1/( 1+ i )2 ]+119,790*[ 1/( 1+ i )3 ]+117,128*[ 1/( 1+ i )4 ] 0=−50,000−86,400*[ 1/( 1+ i ) 1 ]+83,368*[ 1/( 1+ i )2 ]+77,642*[ 1/( 1+ i )3 ]+69,922*[ 1/( 1+ i )4 ]

Escalated dollar ROR for this project is calculated as: i=26.24%, and it is higher than 15% escalated dollar minimum rate of return, i*. So, the project is economically satisfactory.

NPV =-Present value of all costs ( 15% escalated dollar minimum rate of return ) +present value of all revenue ( 15% escalated dollar minimum rate of return )
NPV =− C 0 − C 1 *( P/ F 15%,1 )−O C 2 *( P/ F 15% ,2 )−O C 3 *( P/ F 15%,3 )−O C 4 *( P/ F 15% ,4 ) +Re v 2 *( P/F 15% ,2 )+Re v 3 *( P/ F 15%,2 )+Re v 4 *( P/ F 15% ,4 )
NPV =−50,000−86,400*[ 1/( 1+0.15 )1 ]−37,632*[ 1/( 1+ 0.15 )2 ]−41,148*[ 1/( 1+ 0.15 )3 ] −47,206*[ 1/( 1+ 0.15 )4 ]+121,000*[ 1/( 1+0.15 )2 ]+119,790*[ 1/( 1+ 0.15 )3 ]+ 117,128*[ 1/( 1+ 0.15 )4 ]=
NPV =−50,000−86,400*[ 1/( 1+ 0.15 )1 ]+83,368*[ 1/( 1+ 0.15 )2 ] +77,642*[ 1/( 1+ 0.15 )3 ]+69,922*[ 1/( 1+ 0.15 )4 ]=28,937 dollars

Since NPV at 15% escalated dollar minimum rate of return is positive, we can conclude that the project is economically satisfactory.

Excel screen capture of Escalated dollar analysis. Described in surrounding text
Figure 5-5: Escalated dollar analysis in Microsoft Excel.
Credit: Farid Tayari

Example 5-6:

Now, consider inflation rate of 6% per year for Example 5-5 and make constant dollar analysis.

Constant dollar amounts can be calculated as:

C0=$50,000C1=$86,400*(P/F6%,1)
= 81,509.43		Rev2=$83,368*(P/F6%,2)
= 74,197.22		Rev3=$77,642*(P/F6%,3)
= 65,189.85		Rev4=$69,922*(P/F6%,4)
= 55,385.11
01234

ROR: 0=−50,000−81,509.43*[ 1/( 1+ i )1 ]+74,197.22*[ 1/( 1+ i )2 ]+65,189.85*[ 1/( 1+ i )3 ] +55,385.11*[ 1/(1+ i) 4 ]

ROR for this project is i=19.09%,

For constant dollar analysis, it is necessary to derive constant dollar minimum rate of return, i'*, from escalated dollar minimum rate of return, i*, and inflation rate applying equation 5-2.

i'*=[ ( 1+i* )/( 1+f ) ]−1 i'*=[ ( 1+0.15 )/( 1+0.06 ) ]−1=0.0849=8.49%

Therefore, the constant dollar minimum rate of return, i'*, will be 8.49%.

The constant dollar ROR for this project is calculated as 19.09%, and it is higher than i'* = 8.49%. So, the project is economically satisfactory.

In order to calculate the constant dollar NPV, we have to calculate it at a constant dollar minimum rate of return, i'*= 8.49%.

NPV =−50,000−81,509.43*[ 1/( 1+ 0.849 )1 ]+74,197.22*[ 1/( 1+ 0. 849 )2 ] +65,189.85*[ 1/( 1+0. 849 )3 ]+55,385.11*[ 1/( 1+ 0. 849 )4 ]=$28,937

Constant dollar NPV at i'*= 8.49% is positive, so, the project is economically satisfactory.

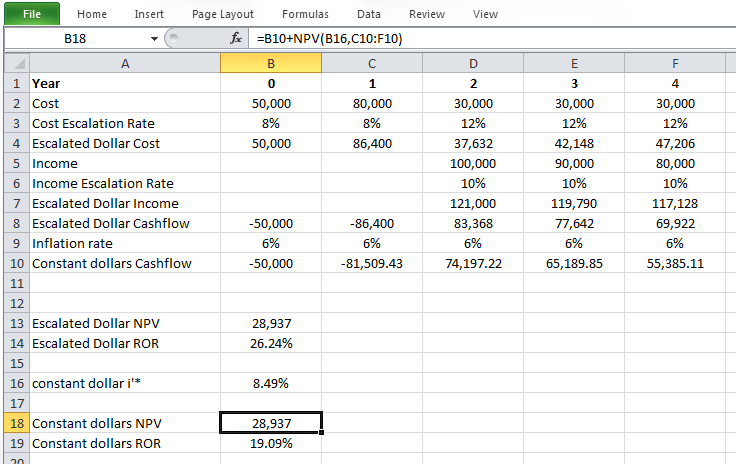
Excel screen capture of constant dollar analysis which is described in surrounding text
Figure 5-6: Constant dollar analysis in Microsoft Excel.
Credit: Farid Tayari

Please watch the following (17:17) video: Escalated and constant dollar ROR and NPV analysis

Escalated and constant dollar ROR and NPV analysis

PRESENTER: Now let's work on a more comprehensive example. And I'm going to use an Excel spreadsheet to work on this example. And this is the data for an investment.

We are going to have investments of $50,000 and $80,000 at the present time and Year 1. We are going to have the revenues of $100,000, $90,000, and $80,000 at Year 2, 3, and 4. And the operating cost is going to be constant at $30,000 from Year 2 to Year 4.

We are going to consider the escalation rate of 8% for the capital cost and 12% for operating costs and 10% of escalation for the revenues. Let's calculate the rate of return and NPV for this investment and calculate the escalated dollar cash flow.

So because we have different escalation rates for our costs and revenue, we need to separate-- we need to keep them separate. The present time capital cost will not be affected by the escalation rate. The $80,000 of capital cost at Year 1 has to be compounded with 8%. And the compounding period is 1.

The $100 revenue at Year 2 has to be compounded by 10%, and the compounding period is 2. The operating cost at Year 2 has to be compounded by 12%, and the compounding period is 2, and so on. Payments are going to be 3 and the compounding period is going to be 4 years. The escalation rate for revenue is 10%, and the escalation rate for operating costs is 12%.

And the result.

So in order to calculate the rate of return, we write the equation for the rate of return, the present value of cost equals the present value of revenue. The present value of costs equals the present value of all capital costs and operating costs that we have here. And the present value of income equals the present value of revenue at Year 2, 3, and 4.

We could also make a summation over each column, considering the negative sign for costs, and calculate the escalated dollar cash flow and write the rate of return equation for that. Both of them are the same. And we solved the equation for i.

And we calculate the rate of return, the escalated dollar cash flow rate of return as 26.24%. So because the calculated rate of return for this project is higher than 15% escalated dollar minimum rate of return, we can conclude that this project is economically satisfactory.

So we can also calculate the NPV for this project. NPV equals the present value of all costs, considering the 15% of escalated dollar minimum rate of return, considering the negative sign, plus the present value of revenue, considering 15% of escalated dollar minimum rate of return. So we calculate the NPV as $28,937. So because this NPV is positive, we can conclude that this project is economically satisfactory.

So let me open the Excel spreadsheet and work on this example. So this is the information for this investment. These are costs. The first two ones are capital costs and the other three are operating costs. As you can see, escalation rates are different. And here, the income.

So now I'm going to calculate the escalated dollar. So for the payment, which is the capital cost at the present time, which will not be affected by the escalation rate, so it is going to be the same payment. Escalated dollar cost at Year 1 can be calculated by compounding this $80,000 by 8% and for 1 year compounding period, so it equals $80,000, multiply 1 plus 8% power 1. So this is the escalated dollar cost at Year 1.

And I can apply to the other cells. For example, the last year, which is going to be an operating cost, has to be compounded by 12% of the escalation rate and 4 compounding periods. F1, which reads it from here.

And then I'm going to calculate the escalated dollar income for our trade incomes in Year 2 to Year 4. So escalated dollar income of $100,000 equals $100,000, multiply 1 plus 10% power 2, because we are going to have two compounding periods. And I apply that to the other revenues.

And now I'm going to calculate the escalated dollar cash flow, which is going to be revenue, the escalated dollar income revenue, minus the escalated dollar cost. I don't have any revenue at the present time, so it will be 0, but I have to write that, minus the costs. And I apply this to the other years.

So this is going to be my escalated dollar cash flow. I am going to calculate the escalated dollar NPV. Because I have a payment at the present time, I have to enter that manually and then use the NPV function for the rest.

The rate was 15%. And then I will choose the cash flow, the rest of the cash flow. So this is escalated dollar NPV and the rate of return. I used the IRR function.

I choose the entire cash flow. And I enter a guess, which I just gave at 10%. And 26.24% is the escalated dollar rate of return.

So this is the escalated dollar cash flow that we just calculated. Now let's consider an inflation rate of 6% per year for this escalated dollar cash flow. And let's calculate the constant dollar cash flow. And then, let's calculate the rate of return and NPV for constant dollar cash flow.

In order to calculate the constant dollar cash flow, we need to discount each payment by the inflation rate, a 6% inflation rate, considering the discounting period. For example, the escalated dollar of $86,400 at Year 1 has to be discounted by 6%, and the discounting period, which is going to be 1, and so on. For Year 2, the discounting period is 2, 6% inflation rate, and so on. And the results.

So this is going to be our constant dollar cash flow. We write the rate of return equation. And we solve the equation for i. And we calculate the constant dollar rate of return as 19.09%.

Now let's calculate the NPV for constant dollar cash flow. But a very important thing here is what rate should be used to calculate the NPV for constant dollar cash flow? We know that the escalated dollar minimum rate of return is 15%. But we cannot use the escalated dollar minimum rate of return for constant dollar NPV calculations.

So what should we do here? We can use the Fisher equation to convert the escalated dollar minimum rate of return into the constant dollar minimum rate of return using the inflation rate. So here is the Fisher equation.

This 15% is an escalated dollar minimum rate of return and a 6% interest rate. The result is going to be 8.49%, which is going to be the constant dollar minimum rate of return. This is the rate that we have to use for calculating our constant dollar NPV.

So we use the constant dollar minimum rate of return of 8.49% to calculate the NPV of constant dollar cash flow. And this is the NPV of constant dollar cash flow. And you can see because this is positive, we can conclude the project is economically satisfactory.

We calculated the constant dollar rate of return as 19.09%. And we need to compare this with the constant dollar minimum rate of return of 8.49% that we just calculated. And because this rate of return is higher than this minimum rate of return, we can also conclude that this project is economically satisfactory.

Now let me open the Excel spreadsheet again. So this is the escalated dollar cash flow. And we are going to consider the 6% of inflation rate for this escalated dollar cash flow. And then we have to calculate the constant dollar cash flow.

In order to calculate the constant dollar cash flow, we need to discount each payment by 6% and the discounting period. So we can leave it as it is, $50,000 of costs. But this escalated dollar cash flow has to be discounted by 1 plus 6%, our discounting period. And then I can apply this to the other years. So for example, the last year, constant dollar cash flow in the last year equals the escalated dollar divided by 1 plus inflation rate power the year.

Now let's calculate the constant dollar NPV. But in order to calculate the constant dollar NPV, we need the constant dollar minimum rate of return. How do we calculate that? I will use the Fisher equation, escalated dollar minimum rate of return, and the inflation rate to calculate the constant dollar minimum rate of return.

So constant dollar minimum rate of return, or i prime star, equals 1 plus 15%, which was escalated dollar minimum rate of return, divided by 1 plus inflation rate, 6%, minus 1, which equals 8.49%. So this 8.49% is the constant dollar minimum rate of return that I can use to calculate the constant dollar NPV.

So I have the constant dollar cash flow here. I have a constant dollar minimum rate of return here. And I can calculate the constant dollar NPV.

So the payment at the present time, I have to enter that manually, plus the NPV function. The rate is a constant dollar minimum rate of return and the rest of the constant dollar cash flow. So because this NPV is positive, I can conclude that the constant dollar cash flow of the project with this constant-dollar cash flow is a good project to invest.

And let's calculate the constant dollar rate of return, which is a fairly straightforward, IRR function. I choose the constant dollar cash flow. I give it a guess, 10%. And this is the constant dollar rate of return, which is 19.09%. And because this constant-dollar rate of return is higher than the constant dollar minimum rate of return, I can conclude that this project is economically satisfactory in terms of rate of return.

So you can also use the Fisher rule to calculate the constant dollar rate of return. Keep it in your mind. It's a very good double-check method to make sure your final result is correct.

So we have the constant-- we have the escalated dollar rate of return here. We have an inflation rate of 6%. So with these two, I should be able to calculate the constant dollar rate of return using the Fisher rule.

So let's see. So the constant-dollar rate of return using the Fisher equation is 1 plus escalated dollar rate of return divided by 1 plus inflation rate of 6% minus 1. And it should give me the exact same value as this rate of return that I calculated here. As you can see, it will be the same.

Credit: Farid Tayari

Summary of calculations:

  1. Step 1: Calculating escalated dollar cash flow using escalation rate and F/P factor
    • Calculating escalated dollar ROR from calculated escalated dollar cash flow in step 1
    • Calculating escalated dollar NPV from calculated escalated dollar cash flow in step 1 and given escalated dollar minimum rate of return, i*
  2. Step 2: Calculating constant dollar cash flow using the given inflation rate and P/F factor from the calculated escalated dollar cash flow in step 1
    • Calculating constant dollar ROR from calculated constant dollar cash flow in step 2
    • Calculating constant dollar minimum rate of return, i'*, from given escalated dollar minimum rate of return, i*, and given inflation rate, f, using Fisher equation
    • Calculating constant dollar NPV from calculated constant dollar cash flow in step 2 and calculated constant dollar minimum rate of return, i'*

Note that the constant dollar NPV is identical to the escalated dollar NPV. Constant NPV equations are mathematically equivalent to escalated dollar NPV equations and then give the same results.

Note that Example 5-4 implicitly assumes the escalation rate is 0% per year. So, for NPV and ROR analysis in Example 5-4, we need to consider a 15% escalated dollar minimum rate of return.

NPV =−50,000−80,000*[ 1/ ( 1+0.15 ) 1 ]+70,000*[ 1/ ( 1+0.15 ) 2 ]+ 60,000*[ 1/ ( 1+0.15 ) 3 ]+50,000*[ 1/ ( 1+0.15 ) 4 ]=1,403

And since it is positive, the project is economically satisfactory.

And calculated ROR (15.61%) is also higher than the 15% escalated dollar minimum rate of return, so we can conclude that the project is economically satisfactory.

Summary and Final Tasks

Summary and Final Tasks ksc17

Summary

Escalated values are also defined as actual, current, then current or nominal dollars. They are always inclusive of the effects of inflation and other parameters including technological, environmental, market, and related issues.

Constant values are escalated values that have had the effects of inflation discounted from them to a base period in time which typically is time zero, but could be any point. Constant dollars are also referred to as real or deflated dollars.

The only difference between escalated and constant values is the inflation rate each year related to the host currency. Consideration of this difference is critical for general geo-resource project evaluation.

Reminder - Complete all of the Lesson 5 tasks!

You have reached the end of Lesson 5! Double-check the to-do list on the Lesson 5 Overview page to make sure you have completed all of the activities listed there before you begin Lesson 6.